
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Semnale sinusoidale. Curenti sinusoidali |
Semnale sinusoidale. Curenti sinusoidali
Semnale sinusoidale. Curenti sinusoidali
Din considerente economice, curentii alternativi variind sinusoidal cu timpul sunt folositi in majoritatea instalatiilor industriale electrice.
Cel mai eficient este un curent alternativ care ramane de aceeasi forma de unda in orice ramura a retelei electrice, oricat de complicata ar fi reteaua. Un astfel de curent este mult mai complet folosit in orice punct chiar daca reteaua contine elemente capacitive si inductive, raspunzatoare pentru modificarea formei de unda prin diferentiere si integrare cum s-a descris in paragraful precedent.
Alt factor important este metoda usoara de producere a curentului alternativ de conductori rotativi cu viteza unghiulara constanta in campul magnetic al masinilor electrice. Aceste masini genereaza un curent periodic.
Singura functie periodica reproductibila la repetate diferentieri si integrari este o functie sinusoidala (si, pentru a fi mult mai exacti, o functie cosinusoidala, intrucat tranzitia la aceasta functie inseamna doar ca faza curentului alternativ a fost modificata printr-un unghi /2). Asadar, curentul alternativ utilizat pentru scopuri industriale este aproape intotdeauna de forma sinusoidala (se considera ca circuitul este alcatuit din elemente liniare; se va arata ca forma de unda a oricarui curent se modifica in elemente de circuit neliniare) descrisa de urmatoarea ecuatie:i = Im sin(t + o)unde Im, = 2f si o sunt cantitati constante (pe viitor toate marimile electrice ce variaza cu timpul: curenti, tensiuni, t.e.m., etc., vor fi notate prin litere mici, ca distinctie de valorile constante ale acestor marimi notate cu litere mari).
O caracteristica a curentilor alternativi care-i face mult mai utilizabili pentru scopuri industriale (fata de curentii continui) este abilitatea lor de a fi usor transformati si distribuiti la consumatori folosind efectul inductiei electromagnetice (transformatoare, etc.). In perspectiva numeroaselor si extensivelor aplicatii ale curentilor sinusoidali, o cunoastere amanuntita a proprietatilor lor de baza este indispensabila. Aceasta cunoastere este de asemenea necesara pentru o mai buna intelegere a comportamentului curentilor de forma complexa in circuite liniare, problema tratata in viitor.
Un curent sinusoidal alternativ este definit prin amplitudinea sa, sau valoarea de varf Im, frecventa f si unghiul de faza sau simplu faza . Faza, in general este un termen care se aplica pentru starea unui proces la un anumit moment de timp. In ingineria electronica, cuvantul este utilizat in conexiune cu curentii sinusoidali pentru a nota o cantitate matematica ce determina in mod neechivoc valoarea curentului la un moment de timp dat (aceasta cantitate fiind variabila independenta sau argumentul functiei trigonometrice). Ca o regula, aceasta cantitate este calculata de la cel mai apropiat punct precedent al undei la care curentul trece prin zero si devine pozitiv. Astfel, faza unui curent sinusoidal (Im =ct.) este exprimata matematic ca t+o si faza initiala la t = 0 este reprezentata prin o.
Faza initiala depinde de punctul de pe unda la care originea timpului (axa de referinta a timpului) a fost aleasa. Spre exemplu, sa consideram ca originea timpului a fost schimbata in urma cu t si in consecinta t este substituit in ecuatie prin t' = t+t. In acest caz sin(t+o) devine sin(t'-t)+o = sint'+(o-t) si faza initiala va fi: o-t
Faza initiala nu este importanta cand investigam un proces cvasi-stationar singular deoarece originea timpului poate fi intotdeauna aleasa astfel ca o-t = 0. Daca ne ocupam de doua sau mai multe procese, originea timpului poate fi aleasa intr-o maniera similara doar pentru unul din procese. Atunci faza initiala a celui de-al doilea proces va diferi, in consecinta de a primului. In astfel de cazuri, procesele sunt cu 'diferenta de faza' sau sunt 'defazate' (out of phase).
|
Pentru doua procese cu aceeasi frecventa:
i1 = I1m sin (t + 1)
i2 = I1m sin (t + 2)
diferenta de faza va fi: t+1) - (t+2) = 1 - 2
Orice deplasare a originii pe axa timpului afecteaza faza initiala o a tuturor proceselor cu un interval egal. Astfel, diferenta lor de faza nu depinde de punctul ales ca origine a timpului.
Pentru a reaminti definitiile altor caracteristici ale curentului alternativ sa spunem ca 'frecventa' este egala cu numarul de cicli completi executati pe secunda si ca inversul sau este 'perioada' (f=1/T); iar amplitudinea este valoarea maxima atinsa de curentul sinusoidal in cursul unei perioade. Evident frecventa si amplitudinea curentului alternativ sinusoidal sunt prin definitie cantitati pozitive.
Pentru a examina (studia) efectele produse de un curent sinusoidal in elemente de circuit: rezistive, inductive si capacitive, vom substitui functia sa i = Im sint in ecuatia vR = iR si in ecuatiile (1.6) si (1.7).
In cazul rezistentei vom avea:
vR = RIm sint = Vm sint
unde am notat: Vm = RIm (1.13a)
In cazul unei bobine inductive (vL= L(di/dt)), gasim:
vL = LIm cost = Vm cost
Vm = LIm = XLIm
unde XL = L (1.13b)
este 'reactanta inductiva' a bobinei.
In cazul unui condensator (vC = 1/C idt + A):
![]()
Vm = Im/(C) = XCIm
unde XC = 1/C (1.13c)
este 'reactanta capacitiva' a condensatorului.
Reactantele capacitive si inductive sunt masurate ca si rezistentele in ohmi (
Valoarea constantei A depinde de punctul undei ales ca origine a timpului, acest punct determinand valoarea tensiunii pe condensator la momentul to:
vC - A = - Im/(C) costo
unde, dupa cum rezulta din solutia integralei definite:
Im/(C) costo = A
Intrucat partea variabila a ecuatiei este independenta de A, vom considera in continuare ca atunci cand t = to constanta A = 0.
In acest caz: vC = -(Im/C) cos
De mare importanta este faptul ca tensiunea aplicata bobinelor inductive sau condensatoarelor difera in faza de curentul ce trece prin aceste elemente de circuit.
Intr-adevar, daca toate ecuatiile de mai sus sunt rescrise pentru aceeasi functie:
- curentul in circuit va fi: i = Im sint
- tensiunea pe rezistenta: vR = vRm sint
- tensiunea pe inductanta: vL = VLm sin(t+/2)
- tensiunea pe condensator:vC = Vcm sin(t-/2)
Dupa cum se poate vedea din aceste ecuatii, tensiunea de pe bobina este deplasata cu un unghi de faza de 90, in avans fata de curent. Acest avans in faza semnifica faptul ca maximul (minimul) de tensiune apare la un moment de timp mai devreme decat cel pentru curent. Tensiunea aplicata pe condensator are de asemenea o deplasare de faza de 90, dar in acest caz tensiunea ramane in urma fata de curent. In ceea ce priveste rezistenta, tensiunea si curentul sau, sunt aratate ca fiind in faza.
Astfel prezentate, reactantele elementelor de circuit XL si XC pot fi tratate ca factori de corelare a valorilor de varf (nu cele instantanee !) pentru curentul si tensiunea sinusoidala. Fiecare din aceste reactante se opun trecerii curentului sinusoidal in acord cu frecventa acestuia: bobina se opune egal cu L, iar condensatorul se opune cu 1/C. La trecerea unui curent continuu ( 0), opozitia unei reactante inductive este nula, iar cea a reactantei capacitive devine infinit de mare. Rezistenta R singura care ramane constanta indiferent de frecventa curentului sinusoidal.
Este indicat sa mentionam aici ca impedanta unei retele multi-ochi continand reactante si conectata la o sursa de curent alternativ nu poate fi calculata facand uz de ecuatiile aplicabile rezistentelor conectate 'serie - paralel' si strabatute de un curent continuu. Aceste ecuatii au fost obtinute din legile lui Kirchhoff prin directa insumare a caderilor de tensiune pe rezistente. In cazul curentilor alternativi cvasi-stationari aceasta poate fi facuta pentru valorile instantanee ale curentului si tensiunii tinand cont de diferenta lor de faza. Astfel, cum am indicat si mai sus, reactantele inductive si capacitive XL = L si XC = 1/C coreleaza doar valorile de varf ale curentilor si tensiunii sinusoidale, fara sa tina cont de diferenta lor de faza. Astfel, reactantele nu pot fi adunate algebric una alteia si apoi rezistentelor retelei. Felul in care aceasta va fi facuta este bine inteleasa referindu-ne la diagrame vectoriale. Deplasarile de faza descrise sunt de mare importanta cand determinam puterea in circuitele de curenti alternativi.
Puterea intr-un circuit de curent alternativ poate fi exprimata in termeni ai puterii dezvoltate in fiecare moment de timp, sau in termeni ai puterii medii pe timp de o perioada (ex.: o perioada intreaga a curentului). Puterea instantanee este egala cu produsul valorilor instantanee ale curentului din circuit si a tensiunii aplicate la bornele circuitului:
p = iv = ImVm sint sin(t+
Pentru aceasta ecuatie originea timpului a fost aleasa astfel ca faza initiala a curentului sau tensiunii sa fie zero. Dupa cum se vede din aceasta ecuatie cand diferenta de faza dintre curent si tensiune este alta decat zero, sunt momente de timp pentru care puterea instantanee p < 0 (devine negativa). La aceste momente directia curentului in circuit este de la potentialul mic la cel inalt si circuitul alimenteaza cu energia inmagazinata de el, sursa de t.e.m., in loc sa consume energie de la ea. Astfel ca lucrul mecanic util realizat de un curent alternativ este evaluat gasind puterea medie P consumata de circuit intr-o perioada. In acest caz, toate momentele la care p < 0 trebuie de asemenea luate in considerare, intrucat componentele corespunzatoare vor fi scazute din suma totala.
Pentru un curent sinusoidal avem:![]()
![]()
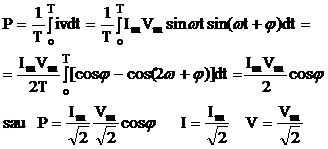
Cantitatile I si V se numesc 'valori efective' ale curentului si tensiunii sinusoidale (rms eff. Vrms V Veff la fel pentru I). produsul acestor valori ale curentului si tensiunii dau puterea disipata sub forma de caldura in circuit sau folosita pentru lucru mecanic de unele dispozitive de circuit. Cand = 0, puterea P = IV corespunde cu cea dezvoltata in circuit de un curent continuu.
Scalele multor instrumente electrice de masura sunt gradate sa citeasca 'valorile efective' (rms) pentru cantitatile masurate. De acum vom folosi valorile efective (rms = root mean square) ale curentului sinusoidal (si altor marimi), cu exceptia cazurilor unde vom considera valorile instantanee ale acestor marimi.
Factorul 'cos ' joaca un rol important in ingineria electronica unde acesta determina eficienta utilizarii echipamentului electric. Pentru a obtine aceeasi putere la cos <1 ca la cos = 1, valorile lui I si V trebuie sa fie corespunzator crescute. Dar instalatiile electrice sunt proiectate sa lucreze la o valoare fixa specifica de tensiune care nu poate fi crescuta, si la un curent limita, peste care creste nepermis disipatia termica.
In consecinta, puterea de iesire a instalatiilor electrice cade sub valoarea calculata cand cos <1 chiar daca I = Im si V = Vm. Astfel este o practica comuna sa indici asa numita 'putere aparenta' (masurata in volti-amperi) S = IV a generatoarelor alternative si a altor dispozitive in loc de puterea utilizata care depinde de proprietatile unui dispozitiv (circuit) distinct (exemplu: de valorile lui cos
Puterea cunoscuta ca activa sau 'true power' este data de: P=IVcos
Unghiul de faza a unui curent alternativ trecand printr-o rezistenta este = 0 si V=I/R. In acest caz puterea activa va fi data de: P=I2R
In circuite realizate doar din inductante si capacitati ideale cos = 0 si puterea medie va fi nula. Aceasta se datoreaza faptului ca aceste elemente de circuit sunt capabile sa stocheze energia de la sursa in campurile lor electrice si magnetice si astfel sa o retransmita sursei de alimentare fara nici o pierdere. Acesta este motivul pentru care acestea sunt numite 'reactive'.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Referate pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||








