
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Robotul - definintie si schema bloc, sistemul mecanic |
Robotul - definintie si schema bloc, sistemul mecanic
1.Robotul. def si schema bloc

Robotul = sistem cu funct
automata, adaptabila prin reprogramare cond mediului complex si
variabil in care actioneaza, amplificand sau inlocuind una sau mai
multe dintre fct umane in actiunea sa asupra mediului.
2.Sistemul mecanic. Structura
Sistemul mecanic al unui robot depinde de tipul robotului: fix sau mobil. Structura mecanica este formata din:
- structura de locomotie, care realizeaza deplasarea robotului
- structura de manipulare, care asigura pozitionarea si orientarea EF.

3.Tipuri de roboti si aplicatii
a) industriali Aplicatii:
sudare;
roboti manipulatori;
vopsire;
paletizare;
metalizare, pentru acoperiri de protectie cu grad ridicat de rezistenta;
turnarea pieselor metalice;
curatirea si debavurarea pieselor turnate;
deservirea masinilor si utilajelor: strunguri, masini de frezat, centre de prelucrare mecanica; masini pentru injectarea maselor plastice; prese pentru stantare si deformare plastica;
montare (asamblarea demontabila a diferitelor produse executate in serie);
controlul calitatii.
b)Paraleli - Au structura formata, in principal, din 2 platforme (fixa si mobila) conectate intre ele prin intermediul mai multor lanturi cinematice. Aplicatiile acestor roboti rezulta din pozitionarea precisa a diferitelor dispozitive datorita miscarilor foarte fine asigurate de mecanismele lant cinematic inchis.
c)Mobili - Aplicatii: manevreaza obiecte, interactioneaza cu oamenii, indeplinesc sarcini in mod independent. Nu executa produse industriale, ci indeplinesc anumite servicii care necesita deplasarea intr-un mediu greu accesibil sau chiar inaccesibil omului(de multe ori).
d) reconfigurabili modulari pot fi utilizati, spre exemplu intr-o linie de productie care are un robot reconfigurabil care intr-o zi impacheteaza anumite produse, iar a doua zi le sorteaza intr-o linie de asamblare, fara a fi necesara interventia unui operator uman pentru comutarea celor doua sarcini; curatirea unor masini sau spatii neaccesibile unui operator uman, cercetarea unor cladiri demolate.
e) Nanoroboti =nanodisp utiliz in scopul mentinerii si protejarii corpului uman impot fact patogeni.
Aplicatii
- Tratamentul bolilor de piele: se utilizeaza o crema care contine nanoroboti.
- Curatirea cavitatii bucale: identifica si sa distruga bacteriile patogene.
- Imbunatatirea sistemului imunitar: pot identifica si distruge bacteriile si virusii.
- Imbunatatirea functionarii sistemului circulator: refac peretii arteriali si arterele, asigurandu-se ca celulele rosii si structurile suport ocupa pozitii corespunzatoare.
f)Medicali - pot fi de laborator, capabili sa execute sarcini spl, sau rob pt interventii chirurgicale, care indeplinesc sarcini complexe si ajuta mediul chirurg sau pot ei insusi sa execute anumite operatii.
g)educationali si de divertisment
- permit explicarea si insusirea notiunilor de robotica intr-un mod practic si simplu
pot fi utilizati si pentru rezolvarea unor probleme de cercetare:
h) Jucarii
4. Roboti industriali
Un robot industrial e def oficial ISO=automatically controlled, reprogrammable, multipurpose manipulator programmable in three or more axes. Cele mai utilizate configuratii de roboti pentru automatizarea industriala sunt cele cu structura articulata, robotii tip SCARA si robotii tip Gantry.
Caracteristicile robotilor industriali sunt:
numarul axelor – comanda completa a situarii efectorului final necesita trei axe pozitionare si trei axe pentru orientare (roll, pitch, yaw sau unghiurile lui Euler).
cinematica – situarea relativa a elementelor si cuplelor cinematice care determina miscarile posibile ale robotului; exista roboti articulati, cartezieni, paraleli si SCARA.
volumul accesibil al spatiului de lucru – regiunea din spatiu pe care o poate atinge robotul.
capacitatea – greutatea maxima ridicata.
viteza – cat de repede poatefi atinsa situarea efectorului final.
precizia – cat de mari sunt erorile de situare fata de situarea comandata.
sursa de putere – motoare electrice, hidraulice, pneumatice.
conducerea – unii roboti conecteaza motoarele de cc prin angrenaje, altii in mod direct.
5.Spatiul de lucru. Spatiul configuratiilor. Spatiul operational
Spatiul de lucru W reprezinta mediul in care evolueaza robotul pentru indeplinirea sarcinii planificate, populat cu obiecte fizice, fixe sau mobile. Spatiul de lucru poate fi modelat ca un spatiu Euclidian Rn, unde n=2 sau 3
Spatiul de lucru util este descris de miscarile tuturor cuplelor cinematice, in limitele definite de motoarele de actionare. Pe tot parcursul miscarii elementelor robotului, efectorul acestuia trebuie sa fie continut in interiorul spatiului de lucru util. Forma spatiului de lucru util este determinata de topologia robotului, de lungimile elementelor, de distributia cuplelor cinematice.
Spatiul
n-dimensional descris de parametrii
de configuratie se numeste spatiul
configuratiilor sau spatiul
coordonatelor cuplelor cinematice si se noteaza cu SC (![]() ):
):
![]() ; n fiind numarul cuplelor cinematice
ale robotului, respectiv numarul gradelor de libertate ale structurii
mecanice a robotului.
; n fiind numarul cuplelor cinematice
ale robotului, respectiv numarul gradelor de libertate ale structurii
mecanice a robotului.
Spatiul
m-dimensional (![]() ,
, ![]() ) descris de coordonatele operationale se numeste spatiu operational
si se noteaza cu S:
) descris de coordonatele operationale se numeste spatiu operational
si se noteaza cu S: ![]() ,unde f este o functie matriceala,
diferentiabila, continua si neliniara, care
transforma vectorul de configuratie
,unde f este o functie matriceala,
diferentiabila, continua si neliniara, care
transforma vectorul de configuratie ![]() in vectorul
coordonatelor operationale
in vectorul
coordonatelor operationale ![]() , in mod unic. Spatiul operational este un
subspatiu, o regiune generalizata a spatiului de lucru.
, in mod unic. Spatiul operational este un
subspatiu, o regiune generalizata a spatiului de lucru.
|
6. Exprimarea situarii efectorului final in spatiul operational
Pt repr situarii EF in spatiul operational se considera un SR fix (atasat bazei robotului daca robotul este fix sau atasat mediului in care evolueaza robotul, daca acesta este mobil), sistemele de referinta atasate elementelor robotului si un sistem de referinta atasat efectorului final.
Pozitia si orientarea efectorului final se exprima cu ajutorul unei matrice de transformare generala 0G, ale carei elemente sunt vectorul de pozitie p si versorii sistemului de referinta atasat efectorului n, o, a:

Exprimarea situarii in spatiul operational se poate realiza prin matricea de transformare generala G sau prin vectorul coordonatelor operationale X:
![]() (2.10)
(2.10)
7. Reprezentari si transformari omogene
Cea mai simpla modalitate de a reprezenta situarea unui obiect, sistemele de referinta si transformarile la care este supusa aceasta situare, avand in vedere comanda miscarilor ce se realizeaza cu ajutorul calculatorului, este reprezentarea matriceala, iar cele mai simple transformari aplicate acestor reprezentari sunt cele omogene (translatie si rotatie).
Intr-un spatiu tridimensional, situarea oricarui obiect este complet precizata daca se poate exprima o matrice de tip general G, ale carei elemente descriu pozitia originii sistemului de referinta atasat corpului si cosinusurile directoare ale versorilor sistemului de referinta atasat obiectului respectiv:
![]()
 ;
;  p este vectorul de pozitie al originii sistemului
atasat obiectului studiat, iar n, o, a sunt versorii sistemului de
referinta atasat.
p este vectorul de pozitie al originii sistemului
atasat obiectului studiat, iar n, o, a sunt versorii sistemului de
referinta atasat.
Daca se considera un obiect oarecare, situarea (pozitia si orientarea) acestuia poate fi exprimata in raport cu un sistem de referinta oarecare x0O0y0z0 printr-o matrice 0G:

8. Transformari omogene. Translatia si rotatia simpla
Transformarea omogena corespunzatoare unei miscari de translatie exprimata prin r0 se exprima prin matricea:
 x0, y0, z0 reprezinta
proiectiile vectorului de translatie
x0, y0, z0 reprezinta
proiectiile vectorului de translatie ![]() pe axele sistemului de
referinta
pe axele sistemului de
referinta
Un
vector ![]() supus unei translatii devine vectorul
supus unei translatii devine vectorul ![]() :
: ![]()
iar
un plan P translatat devine planul P(1) care se determina cu
relatia: ![]()
Daca se aplica transformarea de translatie obiectului a carui situare initiala a fost exprimata prin matricea 0G , situarea rezultata in urma translatiei este data de:

Transformarile omogene simple de rotatie, de unghi oarecare q, in jurul axelor sistemului de referinta, se exprima prin matricele:
rotatia in jurul
axei O0x0:
rotatia in jurul
axei O0y0: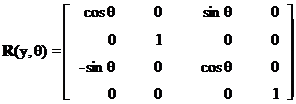
rotatia in jurul
axei O0z0:
Figura
2.7. Rotatii
simple
Un vector r rotit, de exemplu, printr-o transformare
R(x,q) devine:
![]()
Daca se aplica obiectului considerat o rotatie in jurul axei O0x0, situarea transformata a obiectului, exprimata prin matricea G(1) este:
![]() ;
; 

9. Situarea relativa a sistemelor de referinta atasate elementelor robotului
Relatia dintre situarea efectorului robotului in spatiul operational si situarile coordonatelor cuplelor cinematice in spatiul cuplelor cinematice este data de modelul geometric al robotului.
Pentru a exprima situarea (relativa sau absoluta) elementelor robotului, fiecarui element i se ataseaza un sistem de referinta. Situarea relativa a unui sistem in raport cu altul este exprimata printr-o matrice de transformare generala G.
Se
considera un robot cu n grade de
libertate. Exprimand situarea fiecarui element fata de
precedentul se poate descrie situarea efectorului robotului in raport cu orice
element al robotului, respectiv in raport cu baza robotului sau cu sistemul de
referinta fix, daca robotul este mobil, respectiv daca
sistemul de referinta fix nu coincide cu sistemul de
referinta atasat bazei robotului. Situarea elementului (i) in
raport cu elementul (i-1) este exprimata printr-o matrice de transfer ![]() .
.
Situarea
elementului (i) in raport cu baza robotului, considerata ca fiind
elementul (0), se exprima prin matricea ![]() , astfel:
, astfel:![]()
iar
situarea efectorului final in raport cu baza se exprima prin matricea ![]() :
:
![]()
Elementele matricei de transformare G sunt versorii sistemului atasat elementului considerat n, o, a si vectorul de pozitie p al originii sistemului de referinta atasat elementului (efectorului).
Versorii n, o, a au urmatoarele denumiri:
n este versorul normal, defineste axa Ox a sistemului atasat;
o este versorul de orientare, defineste axa Oy a sistemului atasat si are directia determinata de elementele dispozitivului de prindere;
a este versorul de apropiere, defineste axa Oz a sistemului atasat si are directia determinata de deplasarea efectorului.
10. Conventia Denavit-Hartenberg
Etape in Elaborarea modelului geometric al robotului pe baza acestei conventii, aplicabila robotilor cu structura seriala simpla:
a) numerotarea elementelor si cuplelor cinematice ale robotului;
b) alegerea sistemelor de referinta atasate elementelor robotului;
c) stabilirea parametrilor geometrici caracteristici elementelor si cuplelor cinematice;
d) exprimarea mat ![]() ce descriu situarea
relativa a elem (i) in rap cu SR de referinta atasat elem (i-1);
ce descriu situarea
relativa a elem (i) in rap cu SR de referinta atasat elem (i-1);
e) calculul mat ![]() ce descrie situarea
elem (n) in raport cu SR atasat bazei robotului.
ce descrie situarea
elem (n) in raport cu SR atasat bazei robotului.
Alegerea sistemului de referinta ![]() atasat elementului (i) legat de elementul (i-1) prin
cupla de rotatie:
atasat elementului (i) legat de elementul (i-1) prin
cupla de rotatie:
Originea
Oi a sistemului de referinta ![]() este punctul de intersectie dintre perpendiculara comuna
axelor cuplelor (i) si (i+1) si axa cuplei (i+1). Daca axele
cuplelor (i) si (i+1) sunt concurente, Oi poate coincide cu
punctul de concurenta. Daca axele cuplelor (i) si (i+1)
sunt paralele sau coliniare, Oi se alege astfel ca
este punctul de intersectie dintre perpendiculara comuna
axelor cuplelor (i) si (i+1) si axa cuplei (i+1). Daca axele
cuplelor (i) si (i+1) sunt concurente, Oi poate coincide cu
punctul de concurenta. Daca axele cuplelor (i) si (i+1)
sunt paralele sau coliniare, Oi se alege astfel ca ![]() (se alege normala
comuna care trece prin Oi-1 ca axa Ox, iar punctul Oi
rezulta din intersectia acestei normale cu axa cuplei (i+1)).
(se alege normala
comuna care trece prin Oi-1 ca axa Ox, iar punctul Oi
rezulta din intersectia acestei normale cu axa cuplei (i+1)).
Axa ![]() se suprap cu axa
cuplei (i+1). Sensul + este sensul rotatiei trigonometrice in jurul
acestei axe.
se suprap cu axa
cuplei (i+1). Sensul + este sensul rotatiei trigonometrice in jurul
acestei axe.
Axa ![]() are directia
perpendicularei comune la axele cuplelor (i) si (i+1), adica axele
are directia
perpendicularei comune la axele cuplelor (i) si (i+1), adica axele ![]() si
si ![]() .
.
In cazul general, cand
axele ![]() si
si ![]() nu sunt coplanare,
exista o perpendiculara unica.
nu sunt coplanare,
exista o perpendiculara unica.
Daca axele cuplelor
(i) si (i+1) sunt paralele sau coliniare, exista o infinitate de
perpendiculare comune. In acest caz, originea Oi poate fi orice
punct de pe axa cuplei (i+1), iar axa ![]() se alege ca fiind una
din perpendicularele comune celor doua axe, sau o dreapta
perpendiculara, continuta intr-un plan perpendicular pe
directia comuna cu sensul pozitiv astfel incat trecerea de la un
sistem de referinta la altul sa se realizeze cat mai simplu.
Daca normala comuna intersecteaza
se alege ca fiind una
din perpendicularele comune celor doua axe, sau o dreapta
perpendiculara, continuta intr-un plan perpendicular pe
directia comuna cu sensul pozitiv astfel incat trecerea de la un
sistem de referinta la altul sa se realizeze cat mai simplu.
Daca normala comuna intersecteaza ![]() in originea Oi-1,
atunci di este zero. In cazul cand axele
in originea Oi-1,
atunci di este zero. In cazul cand axele ![]() si
si ![]() sunt paralele, unghiul
i este zero.
sunt paralele, unghiul
i este zero.
Daca axele ![]() si
si ![]() sunt concurente, axa
sunt concurente, axa ![]() este normala la planul
determinat de axele
este normala la planul
determinat de axele ![]() si
si ![]() . Sensul pozitiv al axei
. Sensul pozitiv al axei ![]() este arbitrar. In
acest caz, parametrul
este arbitrar. In
acest caz, parametrul ![]() este egal cu zero.
este egal cu zero.
Axa ![]() are directia
si sensul necesare ca sistemul de referinta
are directia
si sensul necesare ca sistemul de referinta ![]() sa fie drept.
sa fie drept.
11. Modelul geometric direct. Modelul geometric invers
Prin identificarea elementelor matricelor din membrul stang si
membrul drept al ecuatiei matriceale ![]() rezulta 12
ecuatii:
rezulta 12
ecuatii:
 (3.8)
(3.8)
Functia
care realizeaza transformarea vectorului de configuratie q in
vectorul coordonatelor operationale X se numeste model geometric direct si se noteaza MGD: ![]() .
.
Exprimarea coordonatelor operationale ca functii de coordonatele cuplelor cinematice conducatoare reprezinta deci modelul geometric direct al robotului:
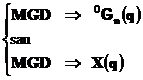

Exprimarea coordonatelor cuplelor cinematice conducatoare ca functii de coordonatele operationale reprezinta modelul geometric invers al robotului sau transformarea coordonatelor:

 (3.10)
(3.10)
Modelul geometric invers are foarte rar o solutie unica. Nu exista o metoda analitica generala pentru determinarea MGI.
12. Metoda Paul pentru determinarea solutiei MGI
Cunoscand
expresia matricei de transformare ![]() de forma:
de forma: ![]()
prin
inmultirea ecuatiei de mai sus cu inversele matricelor ![]() se obtin n ecuatii matriceale, astfel:
se obtin n ecuatii matriceale, astfel:

Elementele matricelor din
membrul stang al acestor ecuatii sunt functii de elementele matricei ![]() si de primele i
variabile ale cuplelor. Elementele matricelor din membrul drept sunt zero,
constante sau functii de variabilele cuplelor de la i+1 la n. Egaland element
cu element matricele din membrul stang cu cele din membrul drept se obtin
cate 12 ecuatii (neliniare, transcendente) din fiecare ecuatie
matriceala, si anume, cate o ecuatie pentru fiecare din
proiectiile celor patru vectori
si de primele i
variabile ale cuplelor. Elementele matricelor din membrul drept sunt zero,
constante sau functii de variabilele cuplelor de la i+1 la n. Egaland element
cu element matricele din membrul stang cu cele din membrul drept se obtin
cate 12 ecuatii (neliniare, transcendente) din fiecare ecuatie
matriceala, si anume, cate o ecuatie pentru fiecare din
proiectiile celor patru vectori ![]() ,
, ![]() ,
, ![]() si
si ![]() .
.
Dintre toate solutiile posibile pentru functiile qi(t) se selecteaza doar cele care satisfac in cele mai bune cond configuratia spatiului de lucru, eliminand solutiile ce conduc la configuratii 'degenerate'.
13. VARIATIA ELEMENTARA A SITUARII EFECTORULUI FINAL
Situarea efectorului final al robotului se exprima prin matricea de transformare generala G. Variatia diferentiala a pozitiei si orientarii efectorului final, datorata erorilor provenite din jocuri, deformatiilor elementelor, vibratiilor, frecarilor intre diferite componente, etc., se noteaza cu dG si reprezinta suprapunerea unei translatii si unei rotatii elementare.
Situarea
rezultata se poate exprima prin:![]()
SR atasat EF
e deci supus unei translatii elementare ![]() si unei
rotatii generale de unghi elementar
si unei
rotatii generale de unghi elementar ![]() , in jurul unei axe oarecare de versor u.
, in jurul unei axe oarecare de versor u.
Situarea
modificata a efectorului: ![]() permite exprimarea
variatiei diferentiale a pozitiei si orientarii EF:
permite exprimarea
variatiei diferentiale a pozitiei si orientarii EF: ![]() ;unde I este matricea unitate.
;unde I este matricea unitate.
Paranteza reprezinta operatorul D, prin intermediul caruia se exprima variatia elementara (diferentiala) a situarii efectorului final. Cele doua transformari care intervin in expresia operatorului D se numesc transformari diferentiale de coordonate. Variatia elementara a situarii efectorului final al unui robot se poate deci determina prin aplicarea operatorului D situarii impuse de sistemul de comanda.
14. Operatorul 0D. Determinarea variatiei elementare ![]()
Operatorul 0D se obtine exprimand matricele transformarilor diferentiale de coordonate.
Matricea de translatie
elementara este de forma:
Matricea de rotatie
elementara :
Pentru calculul matricei ![]() s-au folosit aproximarile: cos d 1, sin d d
s-au folosit aproximarile: cos d 1, sin d d
Operatorul 0D rezulta: 
Structura operatorului 0D reflecta modificarea diferentiala a pozitiei
si orientarii SR AE atasat efectorului. Cei doi vectori care descriu
modificarile elementare reprezinta vectorul de translatie elementara ![]() si vectorul de rotatie elementara
si vectorul de rotatie elementara
![]() :
:
![]() sau
sau ![]()
![]() sau
sau ![]()
Cei
doi vectori ![]() si
si ![]() determina vectorul (elementar) diferential
al miscarii
determina vectorul (elementar) diferential
al miscarii ![]() , exprimat de asemenea in sistemul de referinta
fix.
, exprimat de asemenea in sistemul de referinta
fix.![]()
Aplicand operatorul 0D situarii exprimate prin mat G rezulta variatia diferentiala 0dG in SR fix:


MODELUL DIFERENTIAL AL UNUI ROBOT
Modelul diferential al unui robot descrie relatia dintre variatiile elementare ale coordonatelor operationale si variatiile elementare ale coordonatelor cuplelor cinematice:
![]() ; unde
; unde ![]() (sau
(sau ![]() ) e matricea Jacobiana, a lantului cinematic al robotului.
) e matricea Jacobiana, a lantului cinematic al robotului.
Modelul diferential direct exprima variatiile elementare ale coordonatelor operationale in functie de variatiile elementare ale coordonatelor cuplelor cinematice.
Modelul diferential invers permite calculul variatiilor elementare ale coordonatelor cuplelor cinematice in functie de variatiile elementare ale coordonatelor operationale.
Daca se inlocuieste
calculul diferential cu calculul derivatelor coordonatelor
operationale si ale cuplelor cinematice in raport cu timpul (![]() ) se obtine modelul
cinematic, ce exprima relatia dintre vitezele operationale
si vitezele cuplelor cinematice.
) se obtine modelul
cinematic, ce exprima relatia dintre vitezele operationale
si vitezele cuplelor cinematice.
16.JACOBIANUL UNUI ROBOT. Determinarea Jacobianului din vectorul diferential al miscarii D
Exprimarea modelului diferential presupune determinarea Jacobianului robotului Jr.Calculul Jacobianului robotului se poate realiza in mai multe moduri.
Daca se considera
modelul diferential sub forma ![]() , vectorul diferential al miscarii este chiar
dX. Vectorul deplasarilor elementare din cuplele cinematice ale robotului
este de forma:
, vectorul diferential al miscarii este chiar
dX. Vectorul deplasarilor elementare din cuplele cinematice ale robotului
este de forma:
![]()
iar
Jacobianul robotului este: ![]()
Astfel, modelul diferential
al robotului cu n grade de libertate
se poate scrie:![]()
sau,
explicit: 
Se observa ca: ![]() de unde
rezulta:
de unde
rezulta:
![]()
Deoarece
ccc sunt marimi independente, ![]() , ceea ce conduce la:
, ceea ce conduce la: ![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Esee pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||








