
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Legile fundamentale ale circuitelor |
Legile fundamentale ale circuitelor
Legile fundamentale ale circuitelor
Problemele legate de circuite sau retele de curent continuu, continand doar rezistente pure pot fi usor solutionate recurgand la legea lui Ohm in forma sa generala:
![]()
unde: I curentul in portiunea de circuit electric data
(V1-V2) diferenta de potential pe portiunea de circuit considerata
E t.e.m. totala ce actioneaza in portiunea de circuit data
R rezistenta portiunii de circuit
Aceeasi ecuatie poate fi folosita pentru rezolvarea problemelor circuitului de curent alternativ impunand conditia de cvasi-stationaritate.
Facand uz de ecuatia (1.2) putem analiza modul de lucru al unui circuit complicat construit din n sectiuni sau ramuri, scriind n ecuatii ce contin 2n necunoscute. In sensul rezolvarii acestui set de ecuatii, este necesar de stabilit n conditii independente coreland curentii si tensiunile diverselor ramuri ale circuitului considerat, aceasta se dovedeste adesea a fi o problema foarte complicata.
Analiza circuitelor electrice de orice configuratie si complexitate este mult simplificata prin aplicarea legilor lui Kirchhoff. Prima lege a lui Kirchhoff (a curentului) coreleaza curentii care se intalnesc la un punct de jonctiune sau nod al circuitului si este exprimata matematic ca:

Curentii care intra intr-o jonctiune sunt considerati pozitivi, iar cei ce parasesc jonctiunea negativi.
Legea a doua a lui Kirchhoff (a tensiunii) afirma ca suma algebrica a tuturor caderilor de tensiune pe un circuit simplu inchis (ochi de retea) este egala cu suma algebrica a t.e.m. din acel ochi de retea:
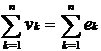
![]()
Aici curentii sunt considerati ca pozitivi daca au sensul unei directii arbitrare de insumare in jurul circuitului (ochiului) considerat iar t.e.m. sunt considerate pozitive daca produc o cadere de tensiune in aceeasi directie.
Ecuatiile ce rezulta din legile lui Ohm si Kirchhoff pot fi de asemenea scrise pentru valorile instantanee ale curentului alternativ cvasi-stationar.
|
In multe cazuri relatia dintre curentul printr-o rezistenta si caderea de tensiune pe aceeasi rezistenta, spre exemplu: caracteristica volt-amperica a unei rezistente i(v) = v/R, poate fi gasita mult mai usor recurgand la metode grafice de calculare. Cand R = ct. caracteristica este o linie dreapta trecand prin origine la un unghi cu axa absciselor si cu tg = i/v = 1/R (fig.1.3a).
Caracteristica unei rezistente neliniare este reprezentata de o curba cu o forma mai mult sau mai putin complicata (fig.1.3b). Modul in care curentul variaza cu timpul poate fi stabilit din caracteristica volt-amperica a rezistentei, eliminand valorile instantanee ale tensiunii de pe axa absciselor si reprezentand valorile instantanee ale curentului in functie de timp. Practic aceasta se obtine aranjand axele de coordonate pentru tensiune si pentru curent paralele cu respectivele axe ale caracteristicii de rezistenta (volt-amperice).
Variatiile de curent si tensiune in circuite complexe pot fi usor reprezentate grafic substituind un grup de rezistente din circuit printr-o rezistenta echivalenta si lucrand cu caracteristica volt-amperica echivalenta. Printr-o rezistenta echivalenta se intelege una care nu afecteaza curentii si tensiunile altor elemente de circuit, orice extensie ar avea in circuitul considerat (analizat).
Caracteristicile echivalente nu sunt utilizate prea des in analiza circuitelor liniare intrucat ecuatiile liniare obtinute din legile lui Kirchhoff pentru aceste circuite sunt usor de rezolvat. Legea de variatie a rezistentei R cu timpul, pentru circuite neliniare, este data uzual intr-o forma tabelata sau prin reprezentare grafica. In astfel de cazuri caracteristicile echivalente sunt foarte utile.
Suplimentar ecuatiilor ce coreleaza curentii, tensiunile si rezistentele din circuit, este necesar de introdus ecuatii pentru calcularea puterii dezvoltate de curentii din circuit. Puterea dezvoltata intr-un circuit se stie ca este determinata prin oricare din urmatoarele ecuatii:
p = iv = v2 / R = i2R
Sa consideram cazul circuitelor pur inductive si capacitive unde legatura dintre curent si tensiune este mult mai importanta ca in circuitele rezistive.
Orice variatie a unui curent intr-o bobina inductiva este stiut ca da nastere la o t.e.m. indusa exprimata matematic ca:
![]()
(O relatie similara se aplica la circuitele cuplate magnetic L M (inductanta mutuala)).
In cazul conectarii unei bobine (inductante) la o sursa externa cu t.e.m. 'e', urmatoarele ecuatii pot fi scrise din legea de tensiune a lui Kirchhoff pentru valorile instantanee ale tensiunilor electromotoare actionand in acest circuit:
e + eL = 0 (1.5)
unde este evident ca: e = L(di/dt).
Prin integrare, putem gasi curentul prin bobina:

Un set similar de ecuatii poate fi scris pentru un circuit pur capacitiv strabatut de un curent i. Orice modificare in tensiunea de pe placile condensatorului este stiut ca produce o modificare corespunzatoare in sarcina q de pe condensatorul de capacitate C:
![]()
Pe de alta parte: dq = idt
Atunci: dvc= (1/C) i dt
de unde diferenta de potential este gasita ca:
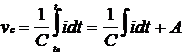 (1.6)
(1.6)
si curentul ca :
![]()
Aceste relatii permit scrierea ecuatiilor legilor lui Kirchhoff, pentru circuite inductive si capacitive de orice configuratie si complexitate.
Formal, consideram ca un curent alternativ produce o cadere de tensiune vL pe bobina inductiva .
In acord cu legea a II-a a lui Kirchhoff:
e = vL
si in consecinta rezulta din ecuatia (1.5) ca:
![]() (1.7)
(1.7)
Pornind de la ecuatia de mai sus, se poate arata ca bobina inductiva (inductanta) are reactanta inductiva nula in curent continuu, deoarece di/dt =0 si vL = 0 cu i = ct. In contrast, condensatorul va fi de reactanta capacitiva infinit de mare la o tensiune continua externa aplicata deoarece dvc/dt = 0 si ic = 0 cand vc = ct.
Derivatele di/dt si dvc/dt iau valori mari in cazul unor curenti si tensiuni rapid variabile in circuite inductive si capacitive. In aceste conditii, reactanta inductiva a bobinei creste cu cat caderea de tensiune vL = L(di/dt) pe ea devine mai mare.
Cand o t.e.m. rapid variabila este aplicata unui condensator, curentul i = C(dvc/dt) creste si in consecinta, reactanta capacitiva scade.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Analize pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||








