
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Problematica rezolvarii problemelor (sisteme rezolutive) |
Problematica rezolvarii problemelor (sisteme rezolutive)
PROBLEMATICA REZOLVARII PROBLEMELOR (SISTEME REZOLUTIVE)
Probleme, rationamente, strategii
Rezolvarea problemelor este obiectivul fiecarui sistem inteligent si se va face atat prin cautarea unor raspunsuri predefinite la unele intrebari, dar mai ales prin procese complexe de deductie, de calcul simbolic si evaluari numerice, care se bazeaza pe faptele specificate in enuntul problemelor si pe fapte inregistrate a priori in baza de cunostinte.
Totalitatea componentelor unui astfel de sistem destinat rezolvarii de probleme formeaza un sistem rezolutiv.
Problema reprezinta o dificultate de natura cognitiva data de:
insuficienta sau inadecvarea unor raspunsuri la intrebari privind o entitate necunoscuta;
incapacitatea sistemului rezolutiv de a construi un raspuns prin aplicarea procedeelor cunoscute.
Problema prezentata spre rezolvare sistemului de inteligenta artificiala este un enunt de problema potentiala. Confirmarea ca problema reala e data de aparitia in cadrul sistemului a unei situatii problematice.
Constituentele primitive ale problemei sunt:
asertiuni ce descriu obiectele ce alcatuiesc universul discursului, numite si date ale problemei (aspectul factual);
asertiuni referitoare la operatiile permise sau conditiile problemei (aspectul procedural);
obiecte, proprietati sau conditii reformulate explicit, consecinta a enuntului sau necunoscutele problemei.
Obiectivul rezolvarii il reprezinta asocierea unei determinari fiecarei necunoscute. Indiferent de modul de rationare utilizat ciclul de baza al unui mecanism de inferente cuprinde patru faze si anume:
faza de selectie a unui subansamblu al bazei de fapte si reguli ce merita atentia fata de restul bazei. Selectia ofera o economie de timp considerabila pentru fazele urmatoare;
faza de filtrare ce are ca efect comparatia intre partea de premisa a regulii considerate si faptele bazei de fapte pentru determinarea regulilor aplicabile;
faza de rezolvare a conflictelor are ca obiectiv alegerea acelor reguli ce sunt aplicate efectiv;
faza de executie consta din aplicarea regulilor alese mai inainte, actiunea constand in general in adaugarea de noi fapte in baza de fapte.
Rationamentul reprezinta constituirea lanturilor sau a retelelor inferentiale intre premise si concluzie. El este fundamentat pe faptele furnizate de enunt si pe cele din baza de cunostinte. Daca acestea sunt suficiente rationamentul este direct, altfel se ajunge la impas si necesita folosirea altor rationamente cum ar fi cel metaforic sau prin analogie.
Rationamentele ce pornesc de la premise la concluzie (se numesc formale) si studiaza transformarile structurale. Rationamentele informale pornesc de la semnificatiile factuale si procedurale cuprinse in enunturi. Aceste metode de rationament surprind interpretari structurale, semnificatii de natura relationala, proprietati primitive, structuri ierarhice bazate pe primitive semantice. Rationamentul informal este necesar sa se valideze prin aplicarea regulilor specifice simbolurilor folosite actual. Desfasurarea rationamentelor are loc pe baza unei strategii ce asigura succesiunea inferentelor.
Iata cateva strategii de control al rationamentelor:
Strategia de control inainte
Aceasta strategie porneste de la starea initiala descrisa de enunt si genereaza succesiv candidati la solutie pana la obtinerea raspunsului corespunzator obiectivului problemei.
Regulile ce se utilizeaza pot fi reguli de inferenta ale mecanismelor logice de baza, reguli specifice definite prin enunt referitoare la generarea termenilor, simboluri relationale, restrictii ce reduc spatiul problemei. Se mai spune despre strategiile de control inainte ca pornesc de la fapte pentru a ajunge la obiectiv. In consecinta se vor selecta regulile a caror parte de conditie este verificata (faza de selectie si filtrare). Pentru faza de rezolvare a conflictelor din ansamblul regulilor selectate se vor alege acelea ce au prioritate maxima. Se obtine astfel strategia generala de control:
< contextul de stare initiala >
regula 1 (operatorul 1)
< contextul de stare succesiva 1>
regula 2 (operatorul 2)
.
regula n (operatorul n)
< contextul de stare finala > s < obiectivul problemei >
Succesiunea regulilor de obtinere a cailor de rezolvare sugereaza un arbore ale carui noduri sunt stari in spatiul starilor, solutia problemei fiind data printr-o procedura de cautare in spatiul starilor. Metodele ce adopta aceasta strategie se numesc metode productive, iar strategia se numeste de jos in sus sau de cautare dirijata prin date.
Se considera un exemplu de baza de cunostinte reprezentata prin reguli de productie:
R1 : IF B and D and E THEN F
R2 : IF D and G THEN A
R3 : IF C and F THEN A
R4 : IF B THEN X
R5 : IF D THEN E
R6 : IF A and X THEN H
R7 : IF C THEN D
R8 : IF X and C THEN A
R9 : IF X and B THEN D
Daca se presupune baza de fapte initiala B, C si obiectivul H, constructia arborelui de decizie pornind de la prima regula prin secventierea regulilor in ordinea in care apar in baza de cunostinte este urmatoarea:

Se considera la acest moment o strategie prin care se selecteaza din multimea regulilor aplicabile acelea pentru care numarul de conditii din partea de premisa este mai mare. Se observa ca regula R8 este preferabila fata de regula R7 intrucat are in premisa doua conditii fata de R7 care are doar una. Cu aceasta strategie se obtine arborele:

Se observa ca printr-o astfel de strategie numarul de inferente se reduce la trei fata de sase anterior. In plus trebuie retinut faptul ca o inferenta aplicata o data nu se mai aplica intrucat nu serveste la nimic ca sa se deduca un fapt ce a fost deja dedus. Eficacitatea ajungerii la scop este data de numarul de inferente necesare, numar de inferente ce depinde in mare masura de faza de eliminare conflicte.
Strategia de control inapoi
Aceasta strategie de control porneste de la obiectivul problemei care prin aplicarea regulilor de descompunere se transforma in subprobleme de complexitate mai mica.
Structura generala a inferentierii este:
< Obiectivul problemei > s < contextul de stare finala >
regula 1
< contextul de stare precedenta 1 >
regula 2
.
regula n
< contextul de stare initiala >
Modul de control specificat mai poarta denumirea si de control dirijat prin obiectivul problemei sau control de sus in jos. Metoda se mai numeste si reductiva.
Rationarea porneste de la scop, selectand acele reguli ce au partea dreapta in corespondenta cu obiectivul problemei. Conditiile necunoscute (partea stanga) devin in acest mod subscopuri ce se vor demonstra. Procesul continua pana cand toate subscopurile se verifica. In acest caz sistemul poate cere utilizatorului sa raspunda la intrebari si procesul reincepe dupa primirea raspunsurilor. In momentul in care sistemul nu mai poate selecta reguli, formula intrebari utilizatorului sau utilizatorul nu mai poate raspunde la intrebari se ajunge la situatia de esec.
Pentru exemplul considerat la strategia de control inainte, se poate observa ca regulile R2 , R3 , R8 pot fi utilizate pentru a verifica scopul A. In acest sens regulile sunt aplicate in ordinea numerotarii lor, pentru a incerca sa verifice din unul in altul subscopurile produse. In caz de esec, cum este subscopul G care nu poate fi dedus, se revine in arbore pentru a selecta regulile lasate la prima trecere. In acest fel explorarea inceteaza atunci cand fie a fost demonstrat obiectivul initial, fie cand toate selectiile posibile au condus la esec. In diversele faze sistemul poate recurge la chestionari ale utilizatorului asupra subobiectivului nerezolvat.
Avantajele strategiei de cautare inapoi:
arborele de cautare este adesea mai putin adanc decat cel aferent strategiei de control inainte;
sistemul poate recurge la intrebari adresate utilizatorului, procesul de rationare fiind interactiv.
Strategia are si un mare dezavantaj legat de faptul ca exista pericolul buclarii.
Strategia de control combinat inainte-inapoi
Aceasta strategie este caracterizata de faptul ca utilizeaza metode reductive pentru descompunerea problemei in subprobleme care apoi sunt rezolvabile prin metode productive, fie prin metode reductive. Succesiunea inversa nu este posibila intrucat metodele productive genereaza de la primul pas candidati la solutie ce nu reprezinta subproblemele, fapt pentru care odata selectata metoda productiva nu poate fi parasita pentru a continua rezolvarea prin alte metode. Deci odata generata o metoda productiva aceasta va fi utilizata pana la obtinerea solutiei finale.
Alegerea strategiei de control este dependenta de tipul de rationament ales. Cert este faptul ca nici o strategie de control nu este buna in orice situatie. Strategia de control inainte este indicata pentru tratarea cunostintelor empirice si este ineficienta pentru probleme complexe. Daca insa unul sau mai multe scopuri trebuie atinse sau verificate este mult mai indicat sa se utilizeze strategia de control inapoi. Rationarea inapoi este indicata in cazul informatiilor incomplete sau cand se poate angaja un dialog cu utilizatorul in vederea imbogatirii sistemului de informatii necesare inferentelor.
Tipuri reprezentative de probleme
Capacitatea de rezolvare a problemelor de catre un sistem inteligent este apreciata dupa usurinta cu care da solutii la probleme ce nu au fost stabilite in prealabil, precizarea lor fiind facuta in momentul incarcarii bazei de cunostinte.
Din punctul de vedere al satisfacerii conditiilor de formulare se pot distinge trei mari categorii de probleme:
probleme bine formulate - sunt acele probleme ce satisfac conditiile de necesitate si suficienta pentru toate componentele din structura, necunoscutele impreuna cu datele alcatuind un model consistent;
problemele incomplet definite - sunt problemele in a caror formulare se poate pune in evidenta lipsa unor date, a conditiilor acestora sau sunt lipsuri in specificarea elementelor vazute ca necunoscute;
probleme gresit formulate - pentru care pot fi puse in evidenta contradictii si inconsistente sau nu pot fi stabilite clar componentele problemei.
Problemele bine formulate pot fi clasificate in :
(1) - probleme de tip interogativ
(2) - probleme de tip predicativ
(3) - probleme de tip inductiv
(1) - O problema de tip interogativ este compusa din trei parti:
ipoteza =I= (alcatuita din date)
procesul =P= (la care sunt supuse datele)
rezultatul =R= (obtinut in urma aplicarii procesului).
Functie de pozitia necunoscutului =X= in componentele problemei se deosebesc probleme interogative de tip IPX, IXR si XPR. Daca toate componentele problemei sunt cunoscute enuntul problemei este de tip IPR si aceasta reprezinta un fapt. Se poate afirma ca atunci cand unul din componentele unui fapt este necunoscut acesta devine o problema.
Problemele de tip IPX au enuntul: "Care este rezultatul X al aplicarii procesului P asupra obiectelor din ipoteza I ?". Rezultatul se obtine prin aplicarea efectiva a procesului P.
Problemele de tip IXR corespund enuntului: "Ce proces X trebuie aplicat asupra obiectelor din ipoteze I pentru a obtine rezultatul R ?". La acest tip se manifesta caracterul creator, rezolvarea putandu-se aborda astfel:
a) pe baza unor reguli euristice de forma:
IF (ipoteza este de tipul I) AND (rezultatul este de tipul R) THEN
se aplica (METODA_1) OR (METODA_2) OR . OR (METODA_n)
b) pe baza rationamentelor prin analogie
c) pe baza unor metode de sinteza procedurala.
Problemele de tip XPR corespund formularii: "Ce obiecte X trebuie sa fie prelucrate de catre procesul P pentru a obtine rezultatul R ?".
Problema poate fi rezolvata direct doar daca P este o bijectie adica stiind ca R = P(X) solutia va fi X = P-1(R). Daca insa P nu este o bijectie atunci abordarea trebuie facuta prin metode reductive.
(2) - Problemele de tip predicativ - se aseamana cu cele interogative, diferenta fiind ca ipoteza si concluzia sunt entitati cu valoare de adevar. Componentele unei probleme de tip predicativ sunt:
ipoteza =I=
procesul inferential =R=
concluzia =C=
Cele trei tipuri de probleme se vor numi astfel:
Problema de tip IPX - denumita si deductie sau derivare. Se intalneste frecvent in aplicarea procedurilor ce vizeaza descompunerea problemelor in subprobleme;
Problema de tip IXC - denumita si demonstratie. Solutia unei astfel de probleme este formata dintr-un lant de inferente ce porneste de la ipoteze si ajunge la concluzie. Aplicarea unui lant inferential este caracteristica sistemelor rezolutive pentru demonstrarea automata a teoremelor.
Problema de tip XPC - denumita si inductie sau invatare din exemple. Solutia presupune descoperirea unor concepte initiale, a cauzalitatii sau a altor premise prin interpretarea rezultatelor ce se obtin pe baza unor reguli de inferenta cunoscute.
(3) - Problemele de tip imperativ. La aceste tipuri de probleme enuntul nu contine necunoscute si nici date de intrare. Rezultatul invocarii procesului este efectul actual, adica producerea rezultatului cunoscut. O astfel de problema se poate descompune uneori in subprobleme de primele doua tipuri.
Problemele incomplet formulate au solutie doar daca in urma aplicarii unor procedee ce nu altereaza specificul problemei din enunt, se obtine o noua formulare ce satisface conditia de buna formulare. Principalele procedee ce se aplica in astfel de cazuri sunt:
reducerea enuntului la o problema bine formulata, ce este facuta prin eliminarea unor elemente lipsite de relevanta ce alterau buna formulare;
completarea enuntului de date transmise prin mostenire, aferente pieselor din enunt, cu date asimilate prin analogie;
descompunerea problemei in subprobleme astfel incat anumite componente sa fie bine formulate;
extinderea obiectivelor problemei asupra clasei ce cuprinde problema initiala, introducerea de obiecte abstracte, a conditiilor suplimentare ce permit reformularea enuntului pentru a satisface conditiile de problema bine formulata.
Este de la sine inteles ca nu se pune problema rezolvarii problemelor incomplet formulate.
Cunoasterea despre problema in procesul rezolvarii
Piesele de cunoastere pot fi clasificate in raport cu potentialul lor de implicare in procesele de rezolvare a problemelor. Primul criteriu de clasificare se refera la rolul jucat de piesa de cunoastere in procesul rezolvarii, in timp ce al doilea criteriu diferentiaza calitativ cunoasterea pentru fiecare dintre roluri.
Pe baza primului criteriu se obtine urmatorul arbore:

Dependentele reciproce dintre diferitele clase ce formeaza piesele de cunoastere pornesc de la cunoasterea factuala ce defineste prototipuri ale unor fapte si instante ce descriu fapte individuale. Asupra pieselor de cunoastere factuala opereaza cunoasterea procedurala ce specifica proceduri e transformare a pieselor de cunoastere factuala. Cunoasterea de control asupra procesului de rezolvare se bazeaza pe piese de cunoastere procedurala si specifica modul de succesiune in care se inlantuie procedurile de transformare pentru obtinerea de noi structuri, modul de succesiune in aplicarea regulilor de inferenta pentru rationamente.
O a doua clasificare se refera la piesele de cunoastere primitive. Se poate considera ca la fiecare nivel pot exista:
piese ale cunoasterii directe;
piese ale cunoasterii deduse, obtinute din primele prin aplicarea regulilor de inferenta.
In domeniile in care cunoasterea depinde foarte mult de experienta personala a specialistilor ce furnizeaza cunoasterea experta (deci domeniul sistemelor-expert), deosebim piese apartinand cunoasterii globale, pentru care exista mai multe opinii convergente si piese ale cunoasterii personalizate, a fiecarui individ.
In continuare se vor trata moduri de reprezentare a problemelor dupa diferite formalisme specifice modurilor de reprezentare a cunostintelor.
Reprezentarea problemelor in limbajul calculului cu predicate de ordinul intai
Transcrierea in formule a enunturilor presupune efectuarea unei analize cu obiectivele:
descompunerea enuntului in piese de cunoastere ce pot fi descrise cu ajutorul predicatelor de ordinul intai;
extragerea caracteristicilor structurale ale teoriei in care se plaseaza problema data;
definirea cunoasterii factuale prin asigurarea de simboluri constante la variabilele predicatelor;
definirea obiectivului problemei cu ajutorul formulelor din calcul cu predicate de ordinul intai.
Enuntul problemei este exprimat in general intr-un limbaj apropiat de cel natural, ce este transcris in formule ale calculului cu predicate de ordinul intai, problema prezentandu-se sistemului rezolutiv in urmatoarea grupare de simboluri:
suportul obiectual ce ataseaza piese de cunoastere ca variabile formale pentru expresii predicative primare;
simboluri functionale formate din piese de cunoastere pentru definirea termenilor din formule;
simboluri predicative ce definesc piese cu valoare de adevar ce descriu proprietati ale obiectelor sau relatii intre obiecte;
fapte - expresii formale ce exprima adevaruri despre obiectele implicate;
obiectivul reprezentat printr-o expresie formala, prin care se exprima ce se urmareste ca rezultat.
Sa consideram urmatorul exemplu de problema:
" Un grup de excursionisti ajung pe malul stang al unui rau ce nu poate fi traversat inot. La acelasi mal se gasesc doi copii cu o barca. In barca poate sa fie la un moment dat un singur excursionist sau doi copii. In final se cere ca grupul excursionistilor sa se gaseasca pe malul drept, iar cei doi copii impreuna cu barca pe malul stang. "
Se propune urmatoarea grupare de simboluri:
Suportul obiectual format din:
multimea copiilor C =
multimea excursionistilor E =
elementul barca
cele doua maluri
Simbolurile predicative ce se vor asocia proprietatilor :
C(x) - x este un copil
E(x) - x este un excursionist
D(x) - x este pe malul drept
S(x) - x este pe malul stang
B(x) - barca este in pozitia xI
T(x, y,
z) - (x) trece cu barca din pozitia (y) in pozitia (z) in
care xIC
E,
y, zI
Faptele sunt organizate in fapte reprezentand conditii ale problemei si fapte relevand proprietati ale obiectelor.
Conditiile si expresiile formale ce definesc problema traversarii sunt:
- Barca ajunsa pe malul drept trebuie readusa pe malul stang numai de catre un copil, un excursionist ajuns pe malul drept va ramane acolo stiind ca numai asa obiectivul problemei poate fi atins. Deci:
i) [D(x) C(x)] B(d) T(x, d, s)
Daca barca este pe malul stang si pe malul drept exista un copil care sa o readuca inapoi atunci un excursionist poate traversa raul
ii) [S(x) E(x)] [D(y) C(y)] B(s) T(x, s, d)
Daca cei doi copii se gasesc pe malul stang acestia pot traversa raul impreuna utilizand barca, fapt ce se exprima prin formula
iii) [S(x) C(x)] [S(y) C(y)] B(s) T(x, s, d) T(y, s, d)
Pozitia barcii dupa o traversare
iv) T(x, y, z) B(z)
In urma unei traversari obiectele traversate vor fi plasate pe malul destinatie
v) T(x, s, d) D(x)
vi) T(x, d, s) S(x)
Daca ambii copii sunt pe malul drept unul dintre ei va trebui sa aduca barca pe malul stang
vii) [D(x) C(x)] [D(y) C(y)] B(d) T(x, d, s)
Faptele care exprima proprietati ale obiectelor sunt date de multimea copiilor, multimea excursionistilor si de pozitia initiala a acestora.
viii) C(c1), C(c2), E(e1), E(e2), . , E(en), S(c1), S(c2), S(e1), S(e2), . , S(en), B(s)
Obiectivele problemei sunt date de pozitia finala a copiilor, barcii si excursionistilor
ix) D(e1) D(e2) D(en)
si
x) S(c1) S(c2) B(s)
Forma generala a formulelor in calculul cu predicate de ordinul intai nu este convenabila pentru aplicarea formulelor cunoscute in logica. In acest sens o serie de transformari sunt aplicate acestor formule pentru a fi aduse la forma convenabila mecanismului de interpretare.
Skolemizarea formulelor
Activitatea de uniformizare a modului de scriere a formulelor se realizeaza in principal dupa urmatoarele etape:
reducerea numarului de conective prin eliminarea implicatiei si echivalentei;
aducerea formulelor la forma normala prenex (cuantificatorii sunt adusi inaintea corpului formulei pe care o prefixeaza);
|
rescrierea formulei ca formula universala prin eliminarea cuantificatorilor existentiali utilizand functiile Skolem;
rescrierea formulelor utilizand forma Skolem conjunctiva, mult mai convenabila pentru demonstrarea automata.
Se spune ca o formula f are o forma Skolem f S ce nu este logic echivalenta, dar este adevarata daca si numai daca f este adevarata.
Reducerea numarului de conective are ca obiect aducerea formulelor la forma convenabila aplicarii regulilor de inferenta. Reamintim ca in teoria inferentelor logice reprezentarea regulilor se face in forma clauzala si anume:
A1 A2 Am ⊢ B1 B2 Bn
ceea ce este echivalent cu
A1 A2 Am B1 B2 Bn
Vom prezenta in continuare reguli de calcul in formule ale limbajului calculului cu predicate de ordinul intai:
Teorema 1. Fie A si B doua formule oarecare. Atunci sunt valabile urmatoarele reguli:
1) (A B) ⊢ (¬A B
2) ¬(A B) ⊢ (A ¬B);
3) (AsB) ↔ (A ¬B) (¬A B
Teorema 2. Daca x este o variabila, iar A, B, A(x) si B(x) formule, dar A si B nu contin aparitii libere ale variabilei x , atunci:
1) ⊢ x (A B(x))sA xB(x);
2) ⊢ x (A(x) B s xA(x) B
3) ⊢ x (A B(x))sA xB(x);
4) ⊢ x (A(x) B s xA(x) B
5) ⊢ x (A(x) B(x))s xA(x) xB(x);
Pornind de la o formula oarecare A se poate gasi o formula A' numita si forma prenex a lui A cu proprietatile:
1) A' este echivalenta cu A, adica ⊢AsA'
2) in formula A', toti cuantificatorii (in cazul cand exista) sunt plasati grupat in partea cea mai din stanga a formulei prefixand corpul formulei in care sunt plasate celelalte simboluri logice ( , ¬, in cazul cand exista) care figurau in scopul fiecarui cuantificator.
Teorema 3. Daca x si y sunt variabile distincte, iar A, B, A(x), B(x) si A(x, y) sunt formule, dar A si B nu contin aparitii libere ale variabilei x si daca x este liber pentru y in A(x, y) (in formulele 5 si 6), atunci:
1) ⊢ x AsA
2) ⊢ x AsA
3) ⊢ x y A(x, y)s y x A(x, y);
4) ⊢ x y A(x, y)s y x A(x, y);
5) x y A(x, y) ⊢ x A(x, x);
6) x A(x, x) ⊢ x y A(x, y);
7) x A(x) ⊢ x A(x);
8) x y A(x, y) ⊢ y x A(x, y);
9) ⊢ x A(x)s x ¬A(x);
10) ⊢ x A(x)s x ¬A(x);
11) ⊢ ¬ x A(x)s x ¬A(x);
12) ⊢ ¬ x A(x)s x ¬A(x);
13) ⊢ x A(x) x B(x)s x (A(x) B(x));
14) ⊢ x A(x) x B(x)s x (A(x) B(x));
15) ⊢A x B(x)s x (A B(x));
16) ⊢A x B(x)s x (A B(x));
17) A x B(x) s x ( A B(x) );
18) A x B(x) s x ( A B(x) );
19) x ( A(x) B(x) ) s x A(x) x B(x);
20) x A(x) x B(x) s x ( A(x) B(x) );
Obtinerea formei prenex are loc dupa urmatoarea succesiune de operatii:
(a) Tranzitarea negatiei de la formule la atomi
TEOREMA 4 Daca x este o variabila, iar A, B, A(x) si B(x) sint formule atunci:
1) x A(x) s x¬A(x);
2) x A(x) s x¬A(x);
3) ¬(A B) s ¬A ¬B;
4) ¬(A B) s ¬A ¬B;
5) ¬¬ A ) s A;
(b) Transferul cuantificatorilor de la formule la atomi
TEOREMA 5 Daca x este o variabila, A(x) si B sint formule cu x libera in A dar legata in B, atunci:
1) x (A(x) B) s x A(x) B;
2) x (B A(x)) s B x A(x);
3) x (A(x) B) s x A(x) B;
4) x (B A(x)) s B x A(x);
5) x (A(x) B) s x A(x) B;
6) x (B A(x)) s B x A(x);
7) x (B A(x)) s B x A(x);
8) x (A(x) B) s x A(x) B;
TEOREMA 6 Daca x este o variabila, A(x) si B(x) sint formule cu x libera atat in A(x) cat si in B(x), atunci:
1) x (A(x) B(x)) s x A(x) x B(x);
2) x (A(x) B(x)) s x A(x) x B(x);
TEOREMA 7 Daca x si y sint variabile A(x, y) si B(x, y) sint formule, x este legata in cel putin una din formulele A(x, y) si B(x, y), iar y este libera atat in A(x, y) cat si in B(x, y), atunci:
1) x y (A(x, y) B(x, y)) s y x (A(x, y) B(x, y));
2) x y (A(x, y) B(x, y)) s y x (A(x, y) B(x, y))
(c) Schimbarea numelor variabilelor
Cand 2 cuantificatori prefixeaza acelasi nume de variabila, numele variabilei este inlocuit cu un simbol diferit de celelalte simboluri pentru variabilele utilizate. Procedeul se mai numeste si standardizarea variabilelor.
(d) Eliminarea cuantificatorului esential
Fie j o formula in limbajul calculului cu predicate de ordinul intai avand variabilele libere x1, x2, ..xn, y. Pentru o variabila oarecare, fie aceasta y, se poate asocia cu simbolul functional fj( x1, x2, ..xn) denumit functia Skolem a lui j, ce satisface axioma Skolem a lui j
x1, x2, ..xn ( y j( x1, x2, ..xn) j( x1, x2, ..xn, fj( x1, x2, ..xn)
Astfel se elimina din formula data cuantificatorul existential prin inlocuirea variabilei cuantificate cu un simbol functional inexistent avand ca argumente acele variabile ce sint cuantificate universal.
(e) Tranzitarea in prefix a cuantificatorilor universali
Intrucat simbolurile de variabile sint individualizate pot fi grupati in prefix toti cuantificatorii universali obtinand astfel forma normala prenex a formulei.
In concluzie, o formula in forma normala prenex este alcatuita din doua parti si anume:
partea din stanga, denumita si prefix, care cuprinde toti cuatificatorii universali ai formulei
partea plasata dupa prefix numita si matricea formulei ce cuprinde literele libere de cuantificatori si alcatuieste corpul propriu-zis al formulei
Forma normala prenex permite transmiterea subformulelor componente in vederea obtinerii formei normale conjuctive, numita si forma Skolem conjunctiva, formata din conjunctii de disjunctii. Daca A, B, C sint formule, atunci:
A ( B C) s (A B) (A C);
(A B) C s (A C) (B C);
Astfel, forma Skolem conjunctiva trebuie eventual simplificata pentru a ajunge la cea mai condensata forma de exprimare a formulei.
Reprezentarea in spatiul starilor
Reprezentarea problemei in spatiul starilor presupune luarea in considerare a starilor si transformarilor acestora datorate unui numar finit de operatori. Reprezentarea se realizeaza prin tripletul
P= ( S, G, R) in care S- reprezinta multimea starilor
G S multimea obiectivelor problemei
R S X S multimea de transformari de stare care indica un drum in "graful problemei"
Se spune ca secventa de stari (s0, s1, . , sn)
formeaza un drum in graf daca sisi+1IR ) i=![]() , iar n-uplul (s0, s1,
. , sn) reprezinta o
solutie a problemei pentru s0
daca snIG
, iar n-uplul (s0, s1,
. , sn) reprezinta o
solutie a problemei pentru s0
daca snIG
Cunoasterea despre problema este definita prin:
multimea obiectivelor abstracte ale problemei;
multimea de operatori;
starea initiala;
starea final;
starea finala formata din stari ce reprezinta obiectivul problemei
Se defineste obiectivul problemei, ca o structura simbolica ce reprezinta o stare de lucruri care odata atinsa confirma faptul ca drumul ce a fost parcurs de la starea initiala prin graful problemei este o solutie. Pot fi stabilite cateva obiective in procesul rezolvarii, si anume:
parcurgerea inainte in spatiul starilor cu scopul atingerii obiectivului
parcurgerea inapoi avand ca scop revenirea la punctele anterioare pentru comutarea procesului de rezolvare pe o alternativa de drum
Informatia de stare contine acele elemente ale cunoasterii prin care:
se asigura tranzitia de la o stare la alta, inainte si inapoi;
se asigura informatia de acces la memorie pentru oricare din starile curente;
se asigura informatia de revenire pentru refacerea starii sistemului in punctele de ramificatie importante ale grafului si selectarea unei alternative in caz de esec;
se asigura informatia de acces la alte trasee ale grafului in situatia prelucrarilor paralele;
pastrarea informatiilor de justificare a pasilor sistemului de rezolvare
Prin spatiul starilor se intelege o multime finita de obiecte implicate in rezolvarea problemei pornind de la starea initiala s0 prin aplicarea unui numar finit de operatori. Aplicarea unui operator asupra unei stari are ca efect producerea unei stari noi sau a unui numar finit de stari alternative. Rezolvarea presupune cautarea in spatiul starilor a unei stari ce corespunde obiectivului problemei. Parcurgerea grafului de la starea initiala s0 la starea finala sn se face prin alegerea unui drum dintr-un numar finit de alternative. In acest proces de parcurgere este cunoscut criteriul de apreciere a obiectivului fara a se cunoaste ordinea de aplicare a operatorilor sau lungimea drumului de parcurs.
Modul de reprezentare in spatiul starilor se face pe baza unei structuri arborescente. Aceasta ridica urmatoarele probleme de rezolvat:
definirea unor reguli restrictive pentru procesul generator de stari avand ca scop eliminarea starilor redundante, a celor care se departeaza de solutie, a combinatiilor absurde ce nu conduc la solutie;
definirea unor strategii de cautare a solutiei in spatiul generat;
definirea unor strategii de revenire in caz de esec;
alegerea unei reprezentari compacte ca spatiu de memorie ocupat;
Se prezinta in continuare problema traversarii raului pentru a carei rezolvare se va utiliza spatiul starilor. Notand cu S si D starile partiale ale problemei ce reprezinta situatia pe cele doua maluri, stang si respectiv drept, se obtine starea ca o reuniune a celor doua "stari potentiale" S D.
Starea initiala: S0=
D0=∅
Starea finala: Sf=
Df=
Operatori: Tcd- un copil traverseaza cu barca pe malul drept
si j=1,2;
T2cd - doi copii traverseaza cu barca pe malul drept
si
Ted- un excursionist traverseaza cu barca pe malul drept
sij=1, n;
Tcs - un copil traverseaza cu barca pe malul stang
dij=1,2;
T2cs - doi copii traverseaza cu barca pe malul stang
di
Tes -un excursionist traverseaza cu barca pe malul stang
di j=1, n;
Prin aplicarea operatorilor definiti mai inainte se poate genera spatiul starilor, spatiul in care prima stare este starea initiala. Modul de formare a arborelui asociat problemei de traversare a raului pentru primele trei nivele este urmatorul:
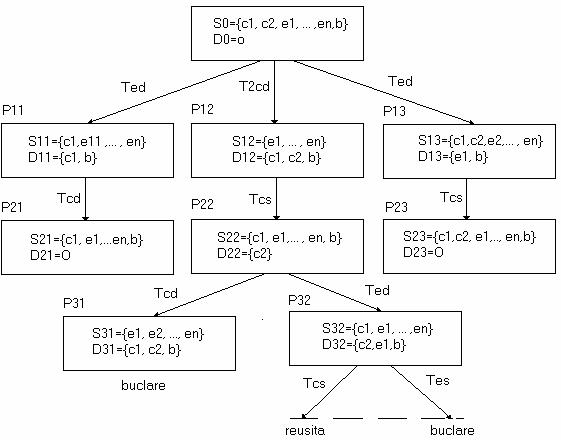
Graful de tranzitie a starilor cu punctul de plecare starea initiala are ramuri ce duc la obiectivul final, operatorii ce conduc la stari redundante fiind eliminate. Solutia problemei poate fi privita fie ca o succesiune de stari, fie ca o secventa a operatorilor ce conduc la starea obiectiv. Furnizarea solutiei ca o secventa de operatori ce conduce la obiectiv va da:
O
In care secventa O''= se repeta de un numar egal cu numarul excursionistilor.
Din analiza reprezentarii in spatiul starilor se observa o asemanare intre aceasta si reprezentarea sistemelor de productie. Altfel, un operator se aplica numai daca anumite criterii prestabilite sint indeplinite de starea asupra careia se aplica (echivalenta cu preconditia), rezultatul aplicarii operatorului fiind obtinerea unei stari noi din cea veche (echivalentul actiunii sau productiei). Strategia de control este cea care determina selectarea operatorilor (regulilor de productie) si a modului de aplicare succesiva a acestora pentru generarea spatiului starilor.
Aplicarea unui operator asupra unei stari fara a putea reveni la starea anterioara pentru a apela un alt operator formeaza strategia de control irevocabila. Strategia de control se numeste tentativa daca la un anumit punct se poate lua decizia de revenire la o stare precedenta in vederea aplicarii de noi operatori. Strategia de control cu revenire (backtracking) este acea strategie prin care punctul de reluare este stabilit din momentul selectarii operatorului, asa ca in caz de esec se poate relua procesul de la un altfel de punct, nu neaparat cel mai apropiat. Strategia de control prin cautare in grafuri este cea prin care se pastreaza informatii privind consecintele aplicarii operatorilor la fiecare pas al generarii.
Utilizarea grafurilor SI/SAU
Aplicarea strategiilor de rezolvare reductive asupra unei probleme P0 porneste de la urmatoarele precizari:
descrierea problemei initiale P0 exprimata in spatiul starilor prin starea initiala P0;
precizarea unei multimi finite de operatori care aplicati asupra problemei produc o multime finita de subprobleme;
precizarea multimii finite a problemei primitive Pp ce sint echivalente cu starile finale in spatiul starilor.
Un graf orientat SI/SAU are urmatoarele caracteristici:
fiecare nod reprezinta o problema sau o subproblema;
nodul initial reprezinta problema P0 ce trebuie rezolvata, nodurile finale reprezinta probleme primitive cu rezolvare cunoscuta, nodurile intermediare reprezentand probleme reduse;
nodul initial este un nod neterminal;
un arc reprezinta un operator de reducere a problemei in subprobleme;
nodurile neterminale pot fi noduri SI cu succesori reprezentand probleme ce trebuiesc rezolvate pentru a se da o solutie nodului predecesor iar nodurile SAU au succesori probleme alternative din care numai una este suficienta pentru a da o solutie nodului predecesor.
Procesul de rezolvare a unei probleme propuse, dupa generarea grafului SI/SAU al reducerii problemei, consta in cautarea in acest graf a conditiilor necesare si suficiente pentru ca nodul initial, reprezentand problema data, sa fie solvabil.
Un nod este solvabil daca este indeplinita cel putin una din conditiile:
nodul considerat reprezinta o problema primitiva (terminal);
nodul considerat este un nod terminal de tip SI, ale carui noduri succesoare sint toate terminale;
nodul considerat este un nod neterminal de tip SAU, iar cel putin unul din succesorii sai este solvabil;
Subgraful continand nodurile solvabile ale unui graf SI/SAU (care reprezinta reducerea unei probleme) in care este continut si nodul initial, demonstreaza solvabilitatea problemei si, de aceea, este denumit graful solutiei.
Riguros, fj (P, L, f, b) un graf orientat cu multimea nodurilor P, multimea arcelor L, f - functia de inaintare si b- functia de revenire, evident f, b: L P. Se spune ca un graf este un arbore daca sint indeplinite conditiile:
1) Graful nu are circularitati
2) Exista un nod p, numit si radacina, pentru care f: L P
Arborii in aplicatiile de IA sint reprezentati cu radacina sus si arcele orientate in jos. Frunzele arborelui sint acele noduri q din P de la care nu pornesc arce spre alte noduri. Caracterizarea cea mai uzuala a adancimii unui nod intr-un arbore este nivelul nodului. Subsetul P1 al punctelor f(xi) din P pentru care
b(x1) = b(x2) =... = b(xn) = p constituie nivelul 1. Atunci:
P1
Setul Pk al punctelor nivelului k este definit succesiv functie de nivelul k-1. Altfel, daca b(xi) I Pk-1, pentru i=1, 2, . , j atunci:
Pk
Evident, pentru descrierea unei probleme intr-un sistem de calcul, este suficient sa se descrie intr-un mod riguros cvadruplul ( P, L, f, b) asociat problemei.
Rezolvarea problemelor prin decompozitie
O strategie de rezolvare a problemelor porneste de la descompunerea acestora in probleme mai simple numite si subprobleme. Daca problema poate fi descompusa in subprobleme, spatiul starilor poate fi reprezentat prin grafuri SI/SAU, si pot fi aplicate metodele de cautare specifice pentru grafuri SI/SAU, metode ce include cautarea prin minimizarea costului, precum si metode de cautare euristica. Jocurile sint probleme tipice reprezentate prin grafuri SI/SAU asa ca o strategie mutare intr-un joc este de fapt redusa la o cautare in graf.
Fie f(n) costul atingerii simbolului terminal de la nodul n. Daca se cosidera ca n este rezolvat prin nodurile fiu n1, n2, . , nm se obtine:
f(n) = max
Daca regulile nu sint aplicate in paralel se obtine pentru costul nodului:
f(n) = f(n1) + f(n2) + . +f(nm) = a f(ni)
Cele doua relatii sint exemple tipice pentru calculul costului atunci cand o problema este descompusa. Una sau alta din aceste formule este practic utilizata la orice problema.
La problemele reprezentate in spatiul starilor este suficient ca un singur nod solutie sa fie atins, pe cand la grafurile SI/SAU procesul descompunerii desface problema in subprobleme.
Pentru rezolvarea problemei corespunzatoare nodului parinte al nodurilor SI, trebuiesc rezolvate toate subproblemele corespunzind nodului fiu ale acestuia. In reprezentarea unui graf SI/SAU, nodurile SI se vor marca prin arce, nodurile nemarcate fiind noduri SAU. Un graf partial este numit graf rezolvent, iar rezolvarea unei probleme reprezentata prin grafuri SI/SAU invoca gasirea tuturor grafurilor rezolvente ale acestuia.
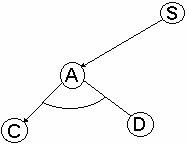
In figura care urmeaza este prezentata o problema complexa A ce poate fi rezolvata prin descompunerea in subproblemele B si C sau prin rezolvarea lui D. In graful respectiv se regasesc ambele tipuri de noduri pentru acelasi parinte.
Se poate introduce un nod suplimentar, pentru separarea nodurilor SI/SAU, pentru care functia de cost este egala cu cea de descompunere a problemei A in subproblema M formata din B si C.
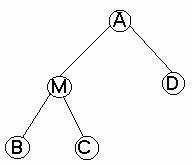
Un nod intr-un arbore SI/SAU poate fi un nod SI al unui nod parinte dat si in acelasi timp un nod SAU al altui nod parinte. Ca urmare, este necesar sa se identifice relatia parinte-fiu. Vom utiliza expresiile "ni este un nod SI al nodului n " sau "nodul ni al lui n este un nod SI".
Cautare in grafuri SI/SAU
Cand se cauta intr-un graf este suficient sa se gaseasca un singur drum, astfel incat daca se cunosc pointerii de la nodurile parinte catre toti fii sai in drumul parcurs, si cautarea este completa, inseamna ca s-a gasit o cale ce constituie o solutie. Totusi un graf rezolvent al grafului SI/SAU este la randul sau un graf. Procesul gasirii solutiei prin cautare corespunde dezvoltarii progresive a solutiei. Numai unele din grafurile rezolvente posibile sint gasite in timpul cautarii. Acestea sint numite grafuri candidate. S-a preferat aceasta denumire in loc de grafuri rezolvente partiale intrucat nu se cunoaste inca daca acestea sint parte a solutiei. Uzual aceste grafuri sint gasite in timpul cautarii si structurile lor trebuiesc reprezentate.
Evaluarea si expandarea grafurilor candidate
Un graf SI/SAU poate fi cercetat prin evaluari si expandari repetate dupa cum urmeaza:
1. Determina daca nodurile grafurilor candidate sint solvabile, insolvabile sau nedecizabile, precum si costul acestora daca este cazul.
2. Expandeaza grafurile candidate.
In primul pas se examineaza
toate punctele finale (nodurile frunza) ale grafului candidat. Daca
acestea sint, noduri terminale ele corespund unei probleme rezolvate si ca
urmare vor fi marcate in acest sens. Daca punctele terminale ale grafului
candidat sint puncte finale ale problemei initiale, dar nu noduri
terminale, problemele corespunzatoare acestor noduri sint insolvabile
si se vor marca
printr-un marker UNSOLVED. Daca nodurile fiu ale unui nod, altele decat
nodurile terminale ale grafului candidat sint noduri SI, si daca toti fii sint SOLVED, atunci nodul
va fi marcat SOLVED. Daca cel putin un
fiu este UNSOLVED atunci nodul parinte va fi marcat UNSOLVED. In cazul in
care nodurile fiu, altele decat punctele terminale sint noduri SAU si cel putin unul a fost
marcat SOLVED atunci nodul parinte va purta aceeasi marca.
Cand nodul S al unui graf candidat devine SOLVED, graful este o solutie a problemei. Daca este necesar calculul costului, se calculeaza costul tuturor nodurilor utilizind costul punctelor finale ale grafurilor candidate. Costul nodului parinte al unui nod SI se calculeaza ca suma tuturor nodurilor sale fiu, pe cand cel al unui nod fiu SAU ca maximul costurilor fiilor. Costul nodului de start este costul nodului grafului candidat. In pasul 2 se gasesc nodurile fiu prin expandarea nodurilor ce sint puncte terminale ale grafului candidat p si nu au fost marcate in nici un fel. Daca nodurile fiu ale nodului expandat n sint noduri SI un nongraf candidat este generat prin adaugarea tuturor nodurilor fiu la nodul p. Daca nodurile fiu ale nodului n sint noduri SAU adaugarea cate unuia din acestea la p va determina generarea mai multor grafuri cate noduri fiu are. In acest mod un numar mare de grafuri candidate vor fi generate prin procesul de cautare.
Cautarea in adincime in grafuri SI/SAU
Ca si in cazul cautarii in grafuri obisnuite, strategiile de cautare in grafuri SI/SAU sint: cautarea in adincime, cautarea in largime, strategii de cautare optimala. Procedura de cautare in adincime este:
Introduce in open_list un graf candidat format doar din nodul de start
While(1)

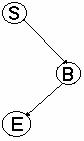
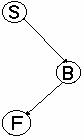
Figura (a) (t1- t4 sint noduri terminale)
In figura b care urmeaza, se arata grafurile candidate in open_list pentru graful SI/SAU din figura a. Cand primul graf candidat din open_list este expandat si evaluat la a treia parcurgere a buclei este gasit UNSOLVED si este mutat din open_list. La a sasea repetare a procedurii graful candidat din open_list este SOLVED si devine solutie a problemei.
![]()
1.
2.
3.

4.
5.


6.
Figura (b): Grafuri in open_list la cautarea in adincime
In aceasta procedura grafurile candidate expandate sint tinute in open_list, insa nu este esential a face acest lucru in cazul cautarii in adancime. Se poate utiliza un sistem in care aceasta lista contine numai un graf partial SOLVED, pentru formarea solutiei trebuie combinat corespunzator cu alte grafuri. Pentru realizarea acestui lucru este necesara construirea unei functii care atunci cand nodurile sint expandate, toate nodurile fiu ale sale au fost generate o singura data. Un singur nod fiu determina un graf partial la un moment dat de timp. Pentru formalizare se defineste functia next_fiu. Se presupune ca nodul n are nodurile fiu n1, n2, . , nm si nodul fiu ni a fost deja generat. Daca nici un nod fiu nu a fost deja generat i=0. Aplicarea functiei next_fiu(n) la nodul n determina urmatorul rezultat:
next_fiu(n)= ni-1 0 i m
null i=m
Cu aceste observatii algoritmul de cautare in adancime in arbori SI/SAU se desfasoara dupa procedura:
Construieste graful candidat p continand numai nodul de start n=s
Evalueaza p
While true
evalueaza p
if n este UNSOLVED elimina n din graful p
n= nod_parinte(n);
Aplicata grafului din figura a anterioara, se obtine secventa S, A, C, F, C, A, S, B, E, t3, E, t4. Secventa de cautare este aceeasi cu cea de cautare in adincime in grafuri obisnuite. Daca in procesul de cautare se obtine ca toate nodurile SAU sint UNSOLVED se intoarce la nodul imediat precedent si continua cautarea dupa alte arce. Acest proces este numit backtracking. Intrucat procedura realizeaza o functie backtracking nu este necesar ca toate nodurile fiu expandate ale unui nod sa fie stocate in open_list. Daca intr-un graf candidat p nodurile fiu ale nodului final n sint intr-un graf candidat p si nodurile fiu ale nodului final n sint noduri SI se adauga toate la graful p. Pentru a reduce timpul cand unul din nodurile fiu este UNSOLVED, n devine UNSOLVED si nu necesita gasirea altor noduri fiu. Pentru a continua procesul se utilizeaza functia next_fiu.
Cautarea solutiei optime in grafuri SI/SAU
Vom trata in continuare gasirea solutiei optime in graf, solutie avand cost minim, cand costul arcelor catre nodurile SAU este definit. Se presupune ca pentru fiecare nod al grafului costul estimat al solutiei este dat. Aceasta corespunde la h' in cautarea pentru grafuri obisnuite. Se va nota costul estimat pentru nodul n cu h'(n). Daca functia euristica h'(n) nu este data, cazul este similar cu h'(n)=0 si algoritmul este identic cu cel de cautare in adancime pentru grafuri SI/SAU.
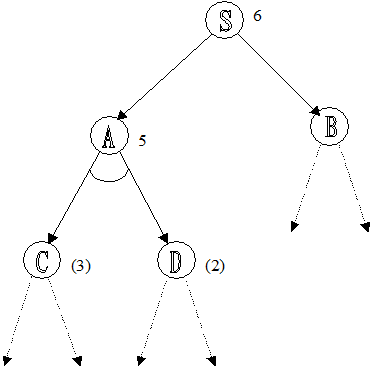
La algoritmul de cautare in adancime descris anterior diferite grafuri candidate au fost generate. Valoarea inferentiala f'(p) a costului unui graf candidat p este obtinuta prin evaluarea lui p utilizand valoarea inferentiala a costului punctelor finale. In figura c se arata o parte a unui graf SI/SAU. Un graf candidat p este desenat prin linii punctate. Costul nodurilor SI se calculeaza utilizand suma costurilor fiilor sai, iar pentru nodurile SAU s-a luat valoarea 1.
![]()
Figura (c)
(intre paranteze s-a prezentat h' si fara paranteze
costurile evaluate).
Daca valorile estimate ale costurilor nodurilor A si S sunt calculate utilizand valorile inferentiale, h'(C)=3 si h'(D)=2 ale punctelor finale C si D din (c), se obtine f'(A)=h'(C)+h'(D), iar pentru S, f'(S)=f'(A)+1. Ca urmare f'(p)=6. Cu algoritmul A cautarea incepe prin expandarea grafurilor cu f'(p) minim. Algoritmul este:
Pune in open_list graful candidat (p) format numai din nodul de start S,
f'(p)=h'(S)
while true
Pentru a ilustra modul in care algoritmul avanseaza se considera exemplul din figura (d), iar in figura (e) se prezinta continutul din open_list prin utilizarea algoritmului de cautare optimala. In figuri s-au trecut intre paranteze costurile estimate, costurile fara paranteze sunt calculate utilizand costuri estimate. Fiecare candidat este denumit (prin marcarea cu Pi), pentru a nu desena de mai multe ori acelasi graf.
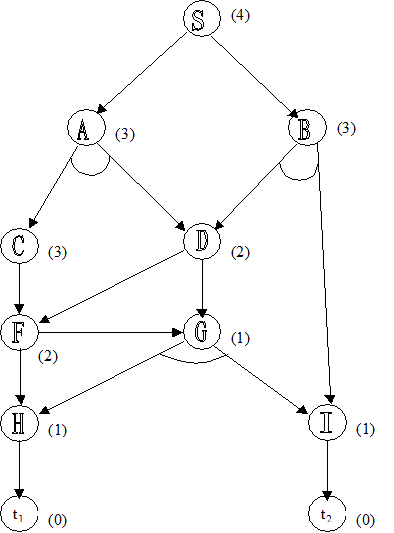
Figura (d) Cautarea solutiei optime in grafuri SI/SAU
In figura (e) sunt aratate numai primele sase cicluri. Dupa ultimul ciclu ilustrat, H si I sunt expandate si nodurile terminale (t1) si (t2) sunt adaugate obtinand graful (p10). Costul pentru (p10) este f(p10)=5. Daca nodurile fiu ale unui nod (n) asociat unui graf candidat (p) sunt noduri SI, ele sunt generate la acelasi moment, cu toate ca sunt evaluate la pasi diferiti. Ca si in cazul utilizarii altor algoritmi, spre exemplu algoritmul A in grafuri obisnuite, acest algoritm nu garanteaza gasirea solutiei optime. Totusi se poate demonstra ca solutia optima este gasita daca h'<h pentru toate nodurile. Daca in calcularea costurilor inferentiale ale grafurilor candidate se seteaza costul tuturor arcelor egal cu (0), aceasta corespunde incercarii de minimizare a viitoarelor costuri de cautare.
|
1. |
P1:
|
|
2. |
P2: |
|
3. |
P3 P4: |
|
4. |
P5: |
|
5. |
P6:
|
|
6. |
P8:
|
Figura (e) Solutia cautarii optimale pentru graful din figura (d)
Cautarea in arbori pentru jocuri
Un domeniu des utilizat in tehnicile de inteligenta artificiala este si cel al teoriei jocurilor. Problema esentiala este cea de luarea deciziei in efectuarea unei noi mutari, ce poate fi rezolvata prin utilizarea tehnicilor de cautare ce au fost deja descrise.
Arbori de jocuri
Sa presupunem ca doi jucatori muta alternativ (operatorii sunt aplicati alternativ), pornind de la o stare initiala, pana cand o stare finala este atinsa. Daca starea finala este un esec sau un succes valoarea evaluata poate fi un scor. Diferitele stari obtinute in timpul parcurgerii jocului pot fi reprezentate asemanator unui graf. De cele mai multe ori aceleasi stari pot fi atinse prin mai multe secvente de mutari. Daca se ignora aceasta si se reprezinta prin noduri distincte, graful este un arbore. In continuare, pentru simplitate, vom reprezenta jocurile prin arbori.
Se presupune ca obiectivul jucatorului care muta primul (numit MAX) este sa obtina valoarea maxima evaluata, iar obiectivul jucatorului care muta al doilea (numit MIN) este de a obtine cea mai mica valoare evaluata. De asemenea, ambii jucatori aleg cea mai buna mutare. In figura (f) este prezentat un arbore simplu asociat, in care nodurile corespunzand lui MAX sunt patrate, iar cele corespunzand lui MIN sunt cercuri. Valorile evaluate sunt date la punctele finale.
In mod normal arborele are o adancime mare si din fiecare nod pleaca mai multe arce. Chiar pentru jocuri de complexitate medie este practic imposibila generarea arborelui incluzand toate punctele finale. In astfel de cazuri, valorile evaluate sunt gasite prin generarea unui arbore in adancime rezonabila, in care evaluarea punctelor terminale ale arborilor partiali se face prin aceleasi metode.

Figura (f) Joc simplu reprezentat ca arbore
Valorile evaluate pe aceasta cale sunt numite valori evaluate static. Daca jocul este aproape de terminare se poate atinge un punct final, insa de cele mai multe ori cea mai buna mutare va fi decisa prin utilizarea valorilor evaluate static. Se ia in considerare faptul ca adversarul determina si el cea mai buna mutare dupa generarea unui arbore partial de adancime corespunzatoare. Adancimea arborelui este restrictionata prin memoria si timpul de calcul necesare. Valorile evaluate static sunt date de cunoasterea caracteristicilor jocului. Pentru a juca SAH, SHOGI sau GO este necesara atat investigarea metodelor de cautare cat si a metodelor de evaluare adecvate. In cele ce urmeaza vor fi prezentate numai metode de cautare pentru cazul in care valorile evaluate sunt considerate cunoscute.
Metoda minimax

Se va explica metoda minimax cu referire la exemplul din figura (f). De la nodul de start S, MAX are de ales intre doua posibilitati. Daca se alege primul arc se ajunge in nodul A. MIN are in continuare doua posibilitati, alegerea nodului D da cea mai mica valoare evaluata. Daca MAX a ales initial nodul B, MIN va alege nodul E care da valoarea inferentiala (1). MAX trebuie sa aleaga propria mutare presupunand ca valoare inferentiala pentru fiecare nod MIN este cea mai mica din valorile evaluate pentru toate nodurile ce pornesc din el. Daca se noteaza nodul MAX cu (n) si fiii sai cu (ni) (i=1.m), iar nodul fiu al fiecaruia cu (nij) (j=1.im), MAX maximizeaza valoarea evaluata a lui f(ni). Selectarea lui (i) va satisface urmatoarea conditie: f(ni)=max f(ni). MIN minimizeaza f(ni) pentru un (i) dat si alege (j) astfel incat f(ni)=min f(nij). Astfel MAX alege (i) in concordanta cu:
f(nij)=max
Daca se ia adancimea arborelui (k), MAX va selecta (iA), asa ca:
f(ni1,i2,.,ik)=max min..
Daca valorile evaluate ale punctelor terminale din arbore sunt corecte, metoda minimax va selecta cea mai buna mutare. Totusi, daca adancimea arborelui creste, numarul nodurilor ce trebuie evaluate creste exponential. Un algoritm mai eficient de rezolvare a acestei probleme se poate obtine utilizand metoda alfa-beta.
Metoda alfa-beta
Fie arborele de cautare din figura (g) in care nodurile sunt numerotate si un scor este dat la fiecare nod terminal. Daca se gasesc cele mai bune mutari utilizand algoritmul minimax, initial MAX alege nodul (1), MIN alege nodul (3), MAX alege nodul (8) ce are valoarea evaluata (5).

Figura (g) Cautarea in arbori folosind metoda alfa-beta
Presupunand
ca intr-o procedura similara cu cea de cautare in adancime
s-a obtinut valoarea evaluata (5) pentru nodul (3), in continuare se
incearca gasirea valorii nodului (4). Se cunoaste in acest
moment faptul ca valoarea nodului (1) nu poate fi mai mare decat (5).
Motivul rezida in faptul ca daca valoarea nodului (4) ar fi mai
mare decat (5), MIN nu va alege nodul (4). Cu toate ca se cunoaste
ca valorile nodurilor (10) si (11) sunt obtinute, valoarea
nodului (4) este cel putin (5). Asa ca nu poate fi mai avantajos
pentru MIN sa aleaga nodul (4) in detrimentul nodului (3). Se deduce
ca MIN va alege nodul (3) fara sa mai examineze nodul (12).
in acest mod valoarea ce determina costul nodului (1) este (5) si ca
urmare valoarea nodului S trebuie sa fie cel putin
(5). Considerand acum ca valoarea evaluata (4) este
obtinuta pentru nodul (5), prin examinarea valorilor tuturor
nodurilor fiu ale sale, si cum selectia nodului (2) nu va aduce
pentru MAX avantaje, nu mai este necesara inspectarea nodului (6) si
a celor care sunt fiii sai. Metoda de segmentare a numarului de
noduri ce sunt cercetate este numita si metoda alfa-beta. Pentru cautarea sistematica a
arborilor care sint adanci metoda este simplu de inteles daca se
formalizeaza dupa cum urmeaza. Se noteaza marginea
inferioara a fiecarui nod cu alfa,
iar marginea superioara cu beta.
In starea initiala pentru nodul S, alfa si beta
sunt - ,
respectiv + .
Pentru aceasta se va scrie ab(S)=( - ).
Daca o valoare (x) este mai mica decat alfa sau mai mare decat beta, se spune ca (x)
depaseste domeniul (a b). Cand valoarea nodului (3) este determinata,
ab(1)
= (- ,5).
Daca se cunoaste ca valorile nodurilor fii ale nodului (1)
depasesc gama (- ,5), conditia pentru intreruperea
cautarii este indeplinita. Cand nodul (11) a fost explorat, ab(4)=(5,b),
deci in afara gamei
(- ,5),
deci conditia de intrerupere a cautarii este din nou
indeplinita si nu va fi necesara cautarea in continuare a
fiilor lui (4). In acest moment ab(1)=(5,5)
si ab(5)=(5, ).
Cand cautarea continua, valoarea nodului (5) este gasita ca
fiind (4), in afara gamei (5, ) si se intrerupe cautarea nodului (2)
si a celor ce pornesc din el.
Prima intrerupere a cautarii apare datorita faptului ca nodul (4) este cel putin egal cu valoarea lui beta si a parintilor sai, a doua intrucat valoarea nodului (2) este cel putin egala cu valoarea lui alfa. Procedeul este denumit beta-cut, respectiv alfa-cut. Metoda de crestere a eficientei cautarii utilizand marginile inferioare si superioare este numita metoda alfa-beta. Pentru a determina eficienta cautarii se calculeaza in cel mai bun caz numarul maxim al nodurilor explorate. Considerand momentul in care s-a gasit valoarea (k) a primului nod fiu de la un nod MAX, nodul (n), atunci ab(n)=(k, ). Daca beta al nodului parinte (m) al lui (n) este mai mic sau egal cu (k), nu este necesara evaluarea celorlalte noduri fiu ale lui (n). Daca nodul (m) nu este primul nod fiu al parintelui sau, valoarea beta este deja data si nu poate fi . Concluzii similare pot fi trase pentru nodurile MIN. In consecinta, in cel mai bun caz, daca nodul (m) nu este primul nod al uni nod parinte, nu este necesara examinarea nici unui nod fiu decat a primului nod al lui (m).
Nodurile terminale sunt reprezentate prin secventa de arce ce le leaga. De exemplu nodul (12) din figura (g) poate fi exprimat prin secventa (1, 2, 3), adica este atins urmarind primul arc al lui S, al doilea de la nodul (1) si al treilea de la nodul (4). Ca urmare nodurile terminale ale arborelui de adancime (k) se exprima prin k-uplul (e1,e2,.,ek). Nodurile ce nu necesita examinarea sunt cele pentru care ei 1, ei+1 1. In consecinta, in cel mai bun caz nodurile care au fost examinate, fie sunt noduri numere pare care au in secventa (1), fie sunt noduri numere impare care au in secventa (1). Notiunea de par sau impar se refera la numarul nodului in adancimea arborelui.
Daca se presupune ca numarul arcelor posibile de la noduri neterminale este (m), atunci numarul nodurilor pare No(k,m) si numarul nodurilor impare Ne(k,m) sunt date prin urmatoarele formule:
daca k este par: No(k,m)=m(k-1)/2, Ne(k,m)=m(k+1)/2
daca k este impar: No(k,m)=Ne(k,m)=mk/2.
Nodul (1,1,.,1) este numarat pentru ambele No(k,m) si Ne(k,m), asa ca Ntotal(k,m) este No(k,m)+Ne(k,m)-1. Cu aceste precizari se obtine:
pentru k par: Ntotal(k,m)=m(k-1)/2+m(k+1)/2-1
pentru k impar: Ntotal(k,m)=2mk/2-1.
In cel mai bun caz, numarul nodurilor ce trebuie examinate prin metoda alfa-beta este aproximativ acelasi cu numarul nodurilor ce trebuie cautat prin metoda minimax intr-un arbore de adancime jumatate.
In cazul cel mai defavorabil toate nodurile vor trebui examinate.
Uzual situatia este cuprinsa intre doua extreme, valoarea reala fiind data prin inegalitatea
mk/2 < N(k,m) <= mk
Utilizarea metodei de cautare in grafuri SI/SAU
Un arbore specific pentru jocuri este reprezentat ca un graf SI/SAU. De exemplu arborele din figura (f) reprezentat ca un graf SI/SAU este aratat in figura (h).

Figura (h) Arbore SI/SAU pentru jocuri
Nodurile fiu ale nodurilor MAX corespund la noduri SAU, cele ale nodurilor MIN la noduri SI (nodul de start este vazut ca un nod SI). Ca si la arborii SI/SAU nodurile terminale au valoarea evaluata data. Costul arcelor este intotdeauna (0). Utilizand metoda minimax, cea mai buna mutare este determinata prin urmatoarele metode:
n daca nodurile fiu ale unui nod dat sunt noduri SI, valoarea nodului este data de cea mai mica valoare evaluata a fiilor sai;
n daca nodurile fiu sunt noduri SAU, valoarea este data de valoarea maxima dintre valorile nodurilor fiu ale sale.
In cazul jocurilor pentru care obiectivul este cel de a face valoarea nodului de start maxima, valorile evaluate sunt in opozitie fata de cost, adica cea mai mare valoare evaluata este cea mai buna. In consecinta metoda de calcul a valorilor in diverse noduri ale grafului este diferita de cea utilizata in metodele descrise anterior pentru arbori SI/SAU.
Valoarea evaluata a nodului terminal a solutiei grafului este insasi valoarea nodului terminal. Valoarea intr-un nod unde fiii sunt noduri SI este valoarea minima din valorile asociate nodurilor fiu. Valoarea unui nod unde fiii sunt noduri SAU este aceeasi cu valoarea nodului fiu. Daca se scrie valoarea nodului (n) ca f(n), f(A)=2 si f(S)=2.
Alte
solutii pot aparea din valorile celorlalte noduri. In cazul de
fata solutia este (1). Metoda descrisa anterior referitoare
la grafuri SI/SAU poate fi
aplicata si la arbori de jocuri. Totusi h'( ) nu este data
de aceeasi formula exceptand nodurile terminale. Pentru a obtine
solutia optima conditia f'(n)
>= f(n) este indeplinita pentru toate nodurile (cand se
urmareste obtinerea solutiei de cost minim
h'(n) <= h(n) pentru toate
nodurile). In consecinta daca valorile punctelor terminale nu
sunt date, valorile inferentiale ale arborilor candidat sunt infinit de
mari. Presupunand ca la expandarea nodurilor neterminale ale grafului
candidat nodurile fiu sunt noduri SI,
ele se expandeaza in acelasi moment. Daca se noteaza primul
nod fiu cu (n1) (nod SI)
al lui (ni), se poate lua f'(n) <= f(n1). Asa se poate
calcula f' si reactualiza in timpul procesului de cautare.
Asemanator cu metoda de cautare optimala descrisa
anterior, principiul acestei metode este bazat pe faptul ca un graf
candidat adus din open_list va fi
expandat dupa cea mai mare valoare inferentiala.
In arbori SI/SAU pentru jocuri gasirea solutiei necesita nu numai nodul terminal care da valoarea solutiei arborelui, ci si drumul urmat pentru ca pornind de la nodul de start acesta sa fie atins. Pentru transpunerea algoritmului, prin conventie se va nota cu EXPL nodurile atinse ce nu au starea SOLVED. In acest context starea nodului (n) este data de tripletul (n, s, v) in care (s) indica faptul ca nodul (n) este SOLVED sau EXPL, (v) da valoarea lui f(n) daca (n) este SOLVED sau f'(n) daca el este EXPL. Starea nodului (n) este pusa in open_list printr-o procedura pe care am notat-o putopen(n, s, v). De asemenea se va scrie pentru nodul parinte parent(n), nodul terminal n ca terminal(n) si pentru a detecta un nod (n) ca fiind SI/SAU s-a utilizat functia type(n). Algoritmul de cautare in astfel de situatii este:
putopen (S,EXPL,f'(n));
while true
/*3*/ if ((S=EXPL) & terminal(n))
putopen (n, SOLVED, min(f'(n), f(n));
/*4*/ if ((S=SOLVED) & (type(n)=AND))
putopen (parent(n), EXPL, f'(n));
/*5*/ if ((S=SOLVED) & (type(n)=OR))
Pentru exemplificarea metodei se considera graful din figura (i):

Figura (i) Cautarea solutiei optime in arbore de joc SI/SAU
Asa cum se vede din tabelul de rezultate, metoda alfa-beta este dependenta de ordinea nodurilor.
|
Pas |
Proc |
Open_list in care S este SOLVED, E este EXPL |
|
1 |
|
(0,E, |
|
2 |
1 |
(1,E, ),(2,E, ),(3,E, |
|
3 |
2 |
(4,E, ),(2,E, ),(3,E, |
|
4 |
1 |
(13,E, ),(14,E, ),(2,E, ),(3,E, |
|
5 |
3 |
(14,E, ),(2,E, ),(3,E, ),(13,S,4) |
|
6 |
3 |
(2,E, ), (3,E, ),(13,S,4),(14,S,4) |
|
7 |
2 |
(7,E, ), (3,E, ),(13,S,4),(14,S,3) |
|
8 |
1 |
(19,E, ), (20,E, ),(3,E, ),(13,S,4),(14,S,3) |
|
9 |
3 |
(20,E, ), (3,E, ),(13,S,4),(19,S,4),(14,S,3) |
|
10 |
3 |
(3,E, ), (13,S,4),(19,S,4),(14,S,3),(20,S,2) |
|
11 |
2 |
(10,E, ), (13,S,4),(19,S,4),(14,S,3),(20,S,2) |
|
12 |
1 |
(25,E, ), (26,E, ),(13,S,4),(19,S,4),(14,S,3),(20,S,2) |
|
13 |
3 |
(26,E, ), (13,S,4),(19,S,4),(14,S,3),(25,S,3),(20,S,2) |
|
14 |
3 |
(26,S,5), (13,S,4),(19,S,4),(14,S,3),(25,S,3),(20,S,2) |
|
15 |
5 |
(10,S,5),(13,S,4),(19,S,4),(14,S,3),(20,S,2) |
|
16 |
4 |
(3,E,5),(13,S,4),(19,S,4),(14,S,3),(20,S,2) |
|
28 |
5 |
(S,S,5),(13,S,4),(19,S,4),(4,S,3),(20,S,2) |
In cazul grafului din figura (i) daca nodul (3) ar fi in locul nodului (1) solutia optima ar fi gasita mult mai rapid. In algoritm au fost notate cele 5 situatii ce sunt ilustrate si in tabelul precedent, pentru a usura cititorul in intelegerea algoritmului.
Spre deosebire de cautarea optimala obisnuita care exploreaza mai intai nodurile cele mai promitatoare si a carei eficienta nu este afectata de aranjarea nodurilor, metoda alfa-beta este dependenta de aceasta. In al doilea rand memoria necesara pentru algoritmul alfa-beta este mult mai redusa. Alegerea uneia din cele doua metode este dependenta de performantele dorite din punctul de vedere al vitezei de calcul si al memoriei necesare
BIBLIOGRAFIE
1. Podaru Vasile, Inteligenta artificiala si siteme expert, Editura Academiei Tehnice Militare, 1997
2. Podaru Vasile, Barnoschi Adriana, Sisteme expert, Editura Academiei Tehnice Militare, 2000, 2004.
3. Ioan Georgescu, Elemente de inteligenta artificiala, Editura Academiei RSR, 1985.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Lucrari pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||









 P3:
P3: 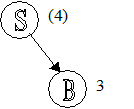

 P4
P4 P7:
P7: 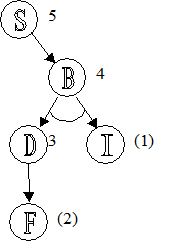 P4
P4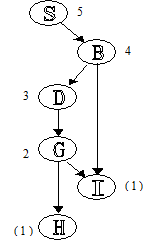 P7P4
P7P4